Slapové tření. Kant a Thomson - Tait
Rotace Země a přitažlivost Měsíce[1]

Thomson-Tait „Natural Philosophy”,[2] I, str. 191 (§ 276): „Na všech nebeských tělesech, která, podobně jako naše Země, mají části svého volného povrchu pokryly tekutinou, existují také nepřímé odpory[3] vlivem tření, brzdícího přílivové a odlivové pohyby. Tyto odpory musí. pokud se tato tělesa pohybují vzhledem k ostatním tělesům, neustále odčerpávat energii jejich relativních pohybů. Tedy jestliže nejprve zkoumáme účinek samého Měsíce na Zemi s jejími oceány, jezery a řekami, pozorujeme. že musí směřovat k vyrovnání period rotace Země okolo její osy a oběhu oněch dvou těles kolem jejich společného těžiště; protože pokud se tyto periody liší, působení přílivu a odlivu na povrchu Země musí neustále odnímat energii jejich pohybu. Abychom prozkoumali problém podrobněji a současně abychom se vyhnuli zbytečným komplikacím, předpokládejme, že Měsíc je homogenní kulové těleso. 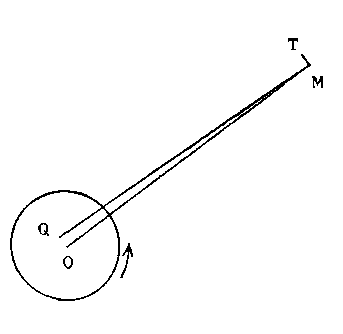Vzájemná akce a reakce přitahování jeho hmotou a hmotou Země se bude rovnat síle působící po přímce jdoucí jeho středem; tato síla musí být taková, že brzdí zemskou rotaci, pokud tato probíhá v kratší periodě, než je pohyb Měsíce okolo Země[4]; musí tedy ležet v nějakém směru, jako je MQ na obrázku, který vystihuje - ovšem nutně s ohromným zvětšením - její odchylku OQ od středu Země. Ale skutečná síla Měsíce ve směru MQ může být považována za složenou z jedné síly ve směru MO ke středu Země, prakticky rovné svou velikostí celé původní síle, a ze síly poměrně velmi malé ve směru MT, kolmé k MO. Tato poslední síla je skoro tečná k dráze Měsíce směrem souhlasným s jeho pohybem. Kdyby taková síla počala náhle působit, musila by předně zvýšit rychlost Měsíce; po určité době by se však Měsíc natolik vzdálil od Země, že by ztratil, pohybuje se proti zemské přitažlivosti, právě tolik rychlosti, kolik předtím získal tečnou zrychlující silou. Nepřetržité působení tečné sily působící ve směru pohybu - i když je tato síla svou velikostí tak malá, že způsobí v každém okamžiku jen nepatrnou odchylku od kruhového tvaru dráhy - má za následek, že se postupně zvětšuje vzdálenost od centrálního tělesa, že vydaná kinetická energie pohybu vykoná stejné množství práce proti přitažlivosti centrální hmoty, jaké samá koná. Co se přitom děje, snadno pochopíme, představíme-li si tento pohyb kolem centrálního tělesa jako spirálu pomalu se rozvíjející ven. Připustíme-li, že síla působí nepřímo úměrně čtverci vzdálenosti, tečná složka gravitace, směřující proti pohybu, bude dvakrát větší než rušící tečná síla, působící ve směru pohybu; a proto jedna polovina práce, konané proti oné první sne, je konána onou druhou silou a druhou polovinu koná kinetická energie odebíraná pohybu. Celkový účinek této zvláštní rušivé příčiny, kterou tu zkoumáme, na měsíční pohyb nalezneme nejsnáze, použijeme-li principu zachování rotační hybnosti. Z toho je patrno, že kolik impulsmomentů se získá v každém časovém intervalu pohyby těžišť Měsíce a Země vzhledem k jejich společnému těžišti, tolik se ztrácí v rotaci Země kolem její osy. Součet impulsmomentů těžišť Měsíce a Země v jejich nynějším pohybu je asi 4,45krát větší než současný moment hybnosti zemské rotace.

Střední rovina prvního pohybu je ekliptika, a proto osy obou těchto momentů jsou k sobě nakloněny o průměrný úhel 23° 27,5 minuty, který, když zanedbáme vliv Slunce na polohu roviny měsíčního pohybu, můžeme vzít za skutečný okamžitý úhel obou os. Výslednice, neboli celý moment hybnosti je proto 5,38krát větší než nynější rotace Země a jeho osa je nakloněna k zemské ose v úhlu 19° 13'. Tedy konečná tendence slapů[5] je převést pohyb Země a Měsíce na prostou rovnoměrnou rotaci s tímto výsledným momentem hybnosti okolo této výsledné osy, jako by Země a Měsíc byly částmi téhož tuhého tělesa: přitom by se vzdálenost Měsíce zvětšila v poměru 1 : 1,46, což je poměr čtverců nynějšího momentu hybnosti těžišť ke čtverci celého momentu hybnosti; a perioda rotace by se zvětšila v poměru 1 : 1,77, což je poměr třetích mocnin těchto momentů. Vzdálenost Měsíce od Země by se tedy zvětšila na 347.100 mil a perioda rotace by se prodloužila na 48,36 dne. Kdyby nebyla ve vesmíru žádná jiná tělesa kromě Měsíce a Země, pak by se mohla takto pohybovat věčně po kruhových drahách kolem svého společného těžiště, při čemž Země by se otáčela kolem své osy v téže periodě a obracela by k Měsíci stále tutéž stranu, takže všechny kapaliny na jejím povrchu by byly v relativním klidu k její tuhé hmotě. Ale existence Slunce brání, aby takový stav byl trvalý. Existovaly by sluneční slapy, dvakrát příliv a dvakrát odliv v periodě zemské rotace relativně k Slunci (t. j. dvakrát během slunečního dne, nebo, což by pak bylo totéž, dvakrát během měsíce). To by se neobešlo bez ztráty energie vlivem tření v kapalině[6]. Není snadné sledovat celý postup poruchy, kterou by tato příčina způsobila v pohybech Země a Měsíce, ale nakonec by donutila Zemi, Měsíc a Slunce otáčet se kolem jejich společného těžiště jako části téhož tuhého tělesa.”

Kant vyslovil roku 1754 po prvé názor, že rotace Země je třením pří přílivu a odlivu zpomalována a že tento účinek bude skončen „teprve, až její (zemský) povrch bude v relativním klidu vzhledem k Měsíci, t. j. až se bude otáčet kolem své osy v téže době, za kterou ji Měsíc oběhne, tedy až bude k Měsíci obracet stále tutéž stranu”[7]. Kant zastával názor, že toto zpoždění děkuje za svůj vznik existenci slapového tření, tedy existenci tekutých hmot na Zemi. „Kdyby Země byla celistvou tuhou hmotou, bez jakýchkoliv tekutin, pak by ani přitažlivost Slunce, ani přitažlivost Měsíce nepůsobila změny v jejím volném otáčení kolem osy; neboť přitahuje jak východní, tak i západní polokouli stejnou silou a nezpůsobuje tak žádnou výchylku na jednu, ani na druhou stranu; ponechává tedy Zemi volnost pokračovat nerušeně v tomto otáčení, jako by neexistovaly žádné vnější vlivy”[8]. S tímto výsledkem se mohl Kant spokojit. K hlubšímu proniknutí do působení Měsíce na zemskou rotaci chyběly tehdy ještě všechny vědecké předpoklady. A vskutku, trvalo to skoro sto let, než Kantova theorie došla všeobecného uznání, a ještě déle, než se poznalo, že příliv a odliv jsou jen viditelnou stránkou působení přitažlivosti Slunce a Měsíce, ovlivňující zemskou rotaci.

Toto obecné pojetí věci bylo právě rozvinulo Thomsonem a Taitem. Přitažlivost Měsíce a Slunce působí nejen na kapaliny zemského povrchu a vnitřku, nýbrž na celou hmotu Země vůbec, brzdíc její rotaci. Pokud se perioda rotace Země neztotožní s periodou oběhu Měsíce kolem Země, potud působí přitažlivost Měsíce - chceme-li se z počátku omezit jen na něj - tak, že se obě periody stále více k sobě blíží. Kdyby byla rotační perioda (relativního) centrálního tělesa delší než oběžná doba satelitu, byla by pozvolna zkracována; je-li kratší, jako je tomu u Země, byla by zpomalována. Ale kinetická energie ani nevzniká z ničeho, ani není na druhé straně ničena. V prvním případě by se satelit přiblížil k centrálnímu tělesu a zkrátil svou oběžnou dobu, v druhém případě by se více vzdálil a svou oběžnou dobu prodloužil. V prvním případě ztratí satelit svým přiblížením k centrálnímu tělesu právě tolik potenciální energie, kolik získalo centrální těleso kinetické energie zrychlenou rotací; v druhém získává satelit zvětšením své vzdálenosti právě tolik potenciální energie, kolik centrální těleso ztrácí kinetické energie své rotace. Celkový součet dynamické (potenciální a kinetické) energie, existující v systému Země-Měsíc, zůstává stejný; tento systém je naprosto konservativní.

Vidíme, že tato theorie je úplně nezávislá na fysikálně-chemickém složení příslušných těles. Odvozuje se z obecných pohybových zákonů volných nebeských těles, jejichž vzájemné působení obstarává přitažlivost v poměru hmot a v obráceném poměru čtverců vzdáleností. Tato theorie vznikla zřejmě jako zobecnění Kantovy theorie o slapovém tření a je nám zde Thomsonem a Taitem dokonce podávána jako její matematické zdůvodnění. Ale ve skutečnosti - a o tom nemají autoři kupodivu ani tušení - vylučuje tato theorie speciální případ slapového tření.

Tření je brzdou pohybu hmoty a bylo považováno po staletí za něco, co ničí pohyb hmoty, tedy kinetickou energii. Víme nyní, že tření a ráz jsou ony dvě formy, v nichž se kinetická energie proměňuje v molekulární energii, v teplo. Při každém tření se tedy kinetická energie jako taková ztrácí, aby se opět objevila ne jako potenciální energie ve smyslu dynamiky, nýbrž jako molekulární pohyb v určité své formě, ve formě tepla. Kinetická energie, ztracená třením, je tedy z počátku opravdu ztracena pro dynamické vztahy příslušného systému. Dynamicky účinnou by se mohla opět stát jen tehdy, kdyby byla z formy tepla proměněna zpět v kinetickou energii.

Jak to nyní bude v případě slapového tření? Je jasné, že také zde celá kinetická energie, udělená masám vody na povrchu Země přitažlivostí Měsíce, je proměněna v teplo, ať už vzájemným třením částic vody následkem její viskosity, nebo třením vody o pevný povrch zemský a rozmělňováním hornin stavějících se přílivu do cesty. Z tohoto tepla se promění zpět v kinetickou energii jen mizivě nepatrná část, která působí při vypařování povrchu vody. Ale také toto mizivě nepatrné množství kinetické energie, postoupené některé části zemského povrchu systémem Země-Měsíc, zůstává zprvu na povrchu Země, podrobeno podmínkám tam platným, a ty připraví veškeré tam působící energii tentýž konečný osud: konečnou proměnu v teplo a vyzáření do vesmíru.

Nakolik tedy slapové tření nesporně brzdí rotaci Země, natolik se kinetická energie na to spotřebovaná pro dynamický systém Země-Měsíc absolutně ztrácí. Nemůže se tedy v této soustavě opět objevit jako dynamická potenciální energie. Jinými slovy: z kinetické energie, spotřebované na brzdění zemské rotace přitažlivostí Měsíce, může se jako dynamická potenciální energie opět plně objevit, t. j. může být kompensována příslušným zvětšením vzdálenosti Měsíce od Země jen ta její část, která působí na tuhou hmotu zeměkoule. Ta část naproti tomu, která působí na kapalné masy Země, může se proměnit v potenciální energii jen tehdy, když neuvede tyto kapalné masy samy v pohyb proti rotaci Země, neboť takový pohyb se proměňuje zcela v teplo a je konec konců vyzářením pro soustavu ztracen.

Co platí o slapovém tření na povrchu Země, platí právě tak o kdysi hypotheticky předpokládaném slapovém tření tekutého jádra Země.

Zvláštní na této věci je to, že Thomson a Tait nepozorují, jak k odůvodnění theorie o slapovém tření vytvořili theorii, která vychází mlčky z předpokladu, že Země je úplně tuhé těleso, a tím vylučuje každou možnost nějakého přílivu a odlivu, a tedy také jejich tření.