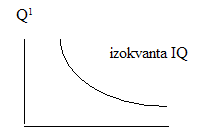
K popisu ekonomické rovnováhy využijeme zjednodušený model 2 x 2 x 2 x 2, tj. 2 vstupy, 2 výrobci, 2 výstupy, 2 spotřebitelé. Jedná se o zjednodušení vhodné, protože z něj lze odvodit vše podstatné, co nás bude zajímat.
Označení:
Q1,Q2 - množství vstupu (zdroje nějakého procesu výroby či výrobního faktoru)
Q1´,Q2´ - množství výstupu (spotřebního statku)
Izokvanta
Izokvanta (IQ) = křivka stejného výnosu. Její průběh je přímým důsledkem zákona klesajících výnosů. Každé úrovni výnosu odpovídá určitá izokvanta, tj. izokvanty tvoří mapu izokvant. Čím je izokvanta vzdálena více severovýchodně od počátku souřadnic, tím vyšší úroveň výnosu představuje.
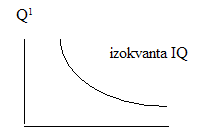
Indiferenční křivka
Indiferenční křivka (IC) = křivka stejného užitku. Její průběh je přímým důsledkem zákona klesajícího užitku. Každé úrovni užitku odpovídá určitá indiferenční křivka, tj. indiferenční křivky tvoří mapu indiferenčních křivek. Čím je indiferenční křivka vzdálena více severovýchodně od počátku souřadnic, tím vyšší úroveň užitku představuje.
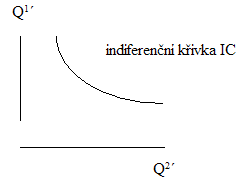
Tvar izokvanty i indeferenční křivky je přímým důsledkem zákona klesajícího výstupu na jednotku vstupu. Snižuje-li se množství jednoho vstupu, zvyšuje se množství druhého vstupu, kterým musí být úbytek prvního vstupu substituován (tj. zvyšuje se jeho cena), tj.:
Klesá-li Q1 či Q1´, pak roste ΔQ1/ΔQ2 (mezní míra technické substituce - MRST), resp. ΔQ1´/ΔQ2´ (mezní míra substituce ve spotřebě - MRSC).
Optimum v případě: 2 vstupy, 1 firma, 2 výstupy
K vyjádření rovnováhy využijeme tzv. krabicový digram:
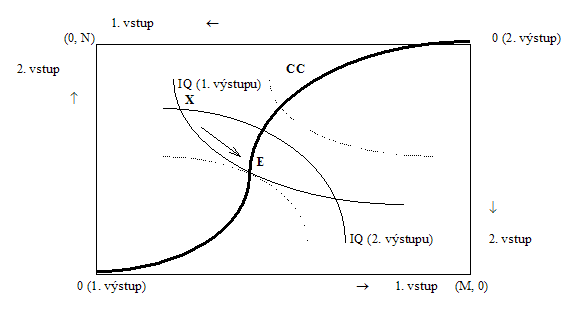
1. Základní prvky grafu:
Levý dolní roh označený jako 0 (1. výstup) můžeme chápat jako počátek souřadnic os, na které vynášíme množství 1. vstupu využitého při výrobě 1. výstupu (horizontálně) a 2. vstupu použitého při výrobě 1. výstupu (vertikálně). Pokud disponujeme zásobou M 1. vstupu a N 2. vstupu, pak koncový bod (M, 0) na horizontální ose představuje situaci, kdy při výrobě 1. výstupu byla použita veškerá zásoba 1. vstupu, a koncový bod (0, N) situaci, kdy při výrobě 1. výstupu byla využita veškerá zásoba 2. vstupu.
Křivka IQ (1. výstup) představuje jednu (z mnoha) izokvant, tj. křivek, které popisují různé kombinace 1. vstupu a 2. vstupu nutné k dosažení určitého množství 1. výstupu. Každému zadanému množství 1. výstupu odpovídá nějaká taková izokvanta. (Další taková izokvanta je naznačena čárkovaně a je rovněž konvexní ve vztahu k počátku 0 (1. výstup), zařazujeme ji do obrázku jen pro ilustraci a bez označení.)
Pravý horní roh označený jako 0 (2. výstup) můžeme chápat jako počátek souřadnic os, na které vynášíme množství 1. vstupu využitého při výrobě 2. výstupu (horizontálně) a 2. vstupu použitého při výrobě 2. výstupu (vertikálně). Jedná se vlastně o zrcadlové převrácení původních souřadnic podle diagonály vymezené koncovými body (M, 0) a (0, N). Tyto koncové body však z hlediska 2. výstupu mají odlišnou (právě opačnou interpretaci).
Křivka IQ (2. výstup) představuje jednu (z mnoha) izokvant, tj. křivek, které popisují různé kombinace 1. vstupu a 2. vstupu nutné k dosažení určitého množství 2. výstupu. Každému zadanému množství 2. výstupu odpovídá nějaká taková izokvanta. (Další taková izokvanta je naznačena čárkovaně a je rovněž konvexní ve vztahu k počátku, kterým je ovšem v zrcadlovém zobrazení roh 0 (2. výstup), v našem obrázku sehraje určitou roli.)
Náš graf se tak skládá ze dvou - prvního a zrcadlově obráceného. První umožňuje zobrazit izokvanty 1. výstupu, druhý umožňuje zobrazit izokvanty 2. výstupu. Jaký je smysl tohoto propojení dvou grafů do jednoho? Abychom tento smysl pochopili (a to je důležité i pro pochopení dalších úvah), musíme si uvědomit, že souřadnice každého bodu uvnitř (i na hranicích) obdélníku v prvním grafu nám říkají, jaká množství jednotlivých vstupů byla využita při výrobě 1. výstupu, a souřadnice v druhém (zrcadlově převráceném) grafu říkají, jaká množství jednotlivých vstupů byla využita při výrobě 2. výstupu. Přitom je zřejmé, že k produkci 1. výstupu a 2. výstupu byla využita celá zásoba obou vstupů. Každý bod uvnitř a na hranici obdélníku tedy popisuje nějaké rozdělení celé zásoby vstupů do výroby dvou výstupů.
2. Nalezení rovnováhy:
Lze předpokládat, že ne každý bod uvnitř a na hranicích plochy obdélníku je bodem, ve kterém jsou vstupy do produkce výstupů rozděleny optimálně (ve smyslu paretovského optima).
Vezměme například bod X. Ten leží na průsečíku jedné z izokvant 1. výstupu a jedné z izokvant 2. výstupu IQ (1. výstup) a IQ (2. výstup). (Není podstatné, že právě těch izokvant, které jsme zobrazili, veškeré další úvahy platí pro libovolný bod, který leží na jakémkoli průsečíku dvou izokvant. Tvrdíme, že tento bod nemůže představovat optimální rozdělení vstupů.
Výše uvedené tvrzení lze snadno dokázat. Pohybujme se po křivce IQ (1. výstup) z bodu X do bodu E (jak ukazuje šipka v grafu). Bod E je zajímavý tím, že se v něm křivka IQ (1. výstup) dotýká s jednou z izokvant popisujících druhý výstup. Po celé trajektorii tohoto pohybu a samozřejmě i v bodě E je produkováno stejně množství 1. výstupu (protože se pohybujeme po izokvantě), dochází jen k jinému rozdělení vstupů (přitom ve smyslu dříve řečené je celá zásoba vstupů vyčerpána).
Pokud si představíme izokvantu 2. výstupu, která prochází bodem X (v našem grafu ji nemáme zakreslenu, protože by tím byl obrázek příliš "přetížen", nepředstavuje však žádnou obtíž si ji domyslet), je zřejmé, že právě v bodě dotyku IQ (1. výstup) s příslušnou izokvantou popisující druhý výstup (v grafu je zakreslena čárkovaně a není zvlášť označena) je při zadaném množství prvního výstupu dosaženo maxima druhého výstupu. To je to, co jsme potřebovali dokázat, tj. že jakýkoli bod, který leží na průsečíku izokvant popisujících v našem grafu dva různé výstupy nemůže být bodem optima a že všechny body na dotyku izokvant popisujících dva různé výstupy mohou být body optima. (Ke stejnému závěru bychom dospěli, pokud bychom se z bodu X posouvali příslušným směrem po křivce IQ (2. výstup); v tomto případě by zůstalo zachováno množství druhého výstupu a zvětšovalo by se množství prvního výstupu.)
Spojíme-li všechny body na dotyku izokvant popisujících různé výstupy získáme tzv. smluvní křivku (CC), která je v grafu vyznačena tučně. (Důvod, proč se tato křivka nazývá "smluvní" bude zřejmé, až se budeme zabývat optimem ve směně.)
Z výše prezentovaného krabicového schématu lze snadno odvodit hranici produkčních možností (křivku PPF), se kterou jsme se setkali již dříve. Představme si mapu izokvant 1. výstupu, kdy každá další izokvanta představuje zvýšení produkce 2. výstupu o jednotku, a mapu izokvant 2. výstupu (odvíjející se od zrcadlového počátku souřednic), kdy se každá izokvanta 2. výstupu dotýká příslušné izokvanty 1. výstupu. Máme tak přesně zadané maximálně možné kombinace dvou výstupů. Pokud je vyneseme do souřadnic jejichž osy vyjadřují množství 1. výstupu a 2. výstupu, dostaneme nám známou PPF. Krabicové schéma popisující situaci 2 vstupy, 1 firma, 2 výstupy lze tedy bez problémů přetransformovat do PPF.
Poznámka:
V této souvislosti lze dát podrobnější zdůvodnění konkávního tvaru PPF směrem k počátku souřadnic. Příčin je několik:
Pokud působí zákon klesajících výnosů při výrobě každého z výstupů (tak tomu nemusí být vždy, zákon klesajících výnosů se může začít projevovat až za hranicí dosažitelných kombinací).
Pokud jsou některé vstupy vhodnější pro výrobu jednoho výstupu a méně vhodné pro výrobu druhého výstupu.
Pokud jsou vyráběné statky různě náročné z hlediska použitých vstupů.
Z výše řečeného vyplývá ještě jeden velmi významný závěr, který je první podmínkou optimální alokace zdrojů: Pokud má být alokace (umístnění) zdrojů v případě 2 vstupy, 1 firma, 2 výstupy optimální, musí být využity všechny zdroje a mezní míra technické substituce (MRTS) vstupů, tj. poměr ve kterém lze při produkci jednoho výstupu zaměnit jeden vstup za druhý, aniž by se změnil výstup, musí být u každého z výstupů stejná.
(To je zřejmé mj. z toho, že v bodě dotyku mají izokvanty obou výstupů stejný sklon, přitom právě tento sklon vyjadřuje poměr, ve kterém lze zaměnit jeden vstup za druhý, aniž by se změnil výstup.)
Optimum v případě: 2 vstupy, 2 firmy, 1 výstup
V tomto případě lze podmínku optima najít poměrně snadno.

Máme grafické vyjádření mezního výstupu z 1. vstupu každé z firem (víme, že mezní výstup s každou další jednotkou vstupu klesá). Nechť v počátečním stavu (1) je mezní výstup 1. firmy větší než mezní výstup 2. firmy. Převodem jedné jednotky 1. vstupu z druhé firmy do první dojde ke zvýšení společného výstupu obou firem. Tak tomu bude až do té doby, dokud se mezní výstupy obou firem nebudou rovnat, tj. pokud nenastane stav (2).
Z výše řečeného vyplývá další významný závěr, který je druhou podmínkou optimální alokace zdrojů: Pokud má být alokace (umístnění) zdrojů v případě 2 vstupy, 2 firmy, 1 výstup optimální, musí být mezní výstup z každého vstupu pro obě firmy stejný.
Optimum v případě: 2 firmy, 2 výstupy
I v tomto případě lze podmínku optima najít poměrně snadno. Jedná se vlastně o nalezení optimální struktury produkce (výstupů) každé z firem v případě že chceme maximalizovat celkový výstup obou firem.
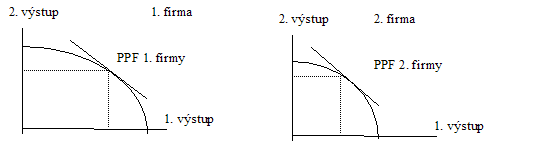
Stačí, když si uvědomíme, že sklon PPF v každém bodě (znázorněný tečnou) v případě obou firem vyjadřuje množství jednoho výstupu, kterého se musíme vzdát, pokud chceme zvýšit výstup druhý. Tento poměr (jak jsme si říkali již dříve) nazýváme mezní mírou transformace produktu (výstupu) - MRTP. Pokud by se mezní míry transformace produktu (výstupu) nerovnaly, lze zvýšit celkové množství produkce tím, že by jedna z firem vyráběla větší množství toho výstupu, u kterého je množství druhého výstupu, který musí obětovat, menší než u druhé firmy; druhá firma by pak zvýšila výrobu výstupu obětovaného první firmou.
Z výše řečeného vyplývá třetí významný závěr, který je třetí podmínkou optimální alokace zdrojů: Pokud má být alokace (umístnění) zdrojů v případě 2 firmy, 2 výstupy optimální, musí být mezní míra transformace výstupu u obou firem stejná.
Optimum v případě: 2 výstupy, 2 spotřebitelé
K vyjádření rovnováhy opět využijeme tzv. krabicový digram. Dlužno dodat, že toto použití je nejtypičtější. Setkáme se zde se všemi typy grafických prvků, pouze jejich interpretace je odlišná. Tento graf popisuje efektivnost směny, tj. umožňuje odlišit ty situace, v nichž si spotřebitelé mohou směnou statků mezi sebou zlepšit svůj užitek, od situací, v nichž není možné pouhým přerozdělením statků zvýšit užitek jednoho ze spotřebitelů aniž by se nesnížil užitek druhého ze spotřebitelů.
Poznámka:
Situaci, kterou graficky znázorníme, si můžeme přiblížit následujícím příkladem. Nechť máme zajatecký tábor, ve kterém každý zajatec dostává každý den nějaké množství čokolády a cigaret. Někteří zajatci jsou ovšem nekuřáci, jiní zase rádi mlsají sladké. Lze očekávat, že si mezi sebou začnou směňovat cigarety za čokoládu, každý tak bude ovšem činit tak, aby si zvýšil svůj užitek.
(Tento příklad není vymyšlený, existence tohoto typu směny se vyskytovala a empirická data, která byla získána, sloužila k potvrzení některých teoretických předpokladů.)
Poznámka 2:
Vzhledem k tomu, že jednotlivé případy hledání optima, kterými se zabýváme, na sebe navazují, budeme pro příslušné dva spotřební statky používat označení 1. výstup a 2. výstup. Oba spotřební statky jsou totiž výstupem produkce nějakých firem.
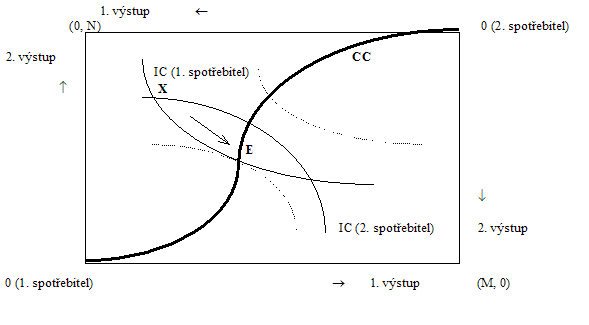
Vzhledem k tomu, že se opět jedná o poměrně náročné schéma, budeme jej "dešifrovat" postupně.
1. Základní prvky grafu:
Levý dolní roh označený jako 0 (1. spotřebitel) můžeme chápat jako počátek souřadnic os na které vynášíme množství 1. výstupu, určitého statku, který byl vyprodukován a který slouží ke spotřebě (horizontálně), a 2. výstupu, určitého statku, který byl vyprodukován a který slouží ke spotřebě (vertikálně). Pokud disponujeme zásobou M 1. výstupu a N 2. výstupu, pak koncový bod (M, 0) na horizontální ose představuje situaci, kdy 1. spotřebitel spotřebovává veškerý 1. výstup a žádný 2. výstup, a koncový bod (0, N) situaci, kdy 1. spotřebitel spotřebovává veškerý 2. výstup a žádný 1. výstup.
Křivka IC (1. spotřebitel) představuje jednu (z mnoha) indiferenčních křivek, tj. křivek, které popisují různé kombinace 1. výstupu a 2. výstupu, při jejichž spotřebě má spotřebitel stejný užitek. Každé úrovni užitku 1. spotřebitele odpovídá nějaká taková indiferenční křivka. (Další taková IC je naznačena čárkovaně a je rovněž konvexní ve vztahu k počátku 0 (1. spotřebitel), zařazujeme ji do obrázku jen pro ilustraci a bez označení.)
Pravý horní roh označený jako 0 (2. spotřebitel) můžeme chápat jako počátek souřadnic os na které vynášíme množství 1. výstupu, který spotřebovává 2. spotřebitel (horizontálně), a 2. výstupu (vertikálně). Jedná se vlastně o zrcadlové převrácení původních souřadnic podle diagonály vymezené koncovými body (M, 0) a (0, N). Tyto koncové body však z hlediska 2. spotřebitele mají odlišnou (právě opačnou interpretaci).
Křivka IC (2. spotřebitel) představuje jednu (z mnoha) jeho IC. Všechny tyto IC tvoří indiferenční mapu. (Další taková IC je naznačena čárkovaně a je rovněž konvexní ve vztahu k počátku, kterým je ovšem v zrcadlovém zobrazení roh 0 (2. výstup), v našem obrázku sehraje určitou roli.)
Náš graf se tak skládá ze dvou - prvního a zrcadlově obráceného. První umožňuje zobrazit IC 1. spotřebitele, druhý umožňuje zobrazit IC 2. spotřebitele. Jaký je smysl tohoto propojení dvou grafů do jednoho? Abychom tento smysl pochopili (a to je důležité i pro pochopení dalších úvah), musíme si uvědomit, že souřadnice každého bodu uvnitř (i na hranicích) obdélníku v prvním grafu nám říkají, jaká množství jednotlivých výstupů, tj. nějakých spotřebních statků spotřebovává 1. spotřebitel, a souřadnice v druhém (zrcadlově převráceném) grafu říkají, jaká množství jednotlivých výstupů spotřebovává 2. spotřebitel. Přitom je zřejmé, že oba spotřebitelé spotřebovávají v každém bodě celou zásobu obou výstupů. Každý bod uvnitř a na hranici obdélníku tedy popisuje nějaké rozdělení celé zásoby dvou spotřebních statků mezi dva spotřebitele.
2. Nalezení rovnováhy:
Lze předpokládat, že ne každý bod uvnitř a na hranicích plochy obdélníku je bodem, ve kterém jsou spotřební statky rozděleny optimálně (ve smyslu paretovského optima).
Vezměme například bod X. Ten leží na průsečíku jedné z IC 1. spotřebitele a jedné z IC 2. (Není podstatné, že právě těch IC, které jsme zobrazili, veškeré další úvahy platí pro libovolný bod, který leží na jakémkoli průsečíku dvou IC různých spotřebitelů. Tvrdíme, že tento bod nemůže představovat optimální rozdělení výstupů.
Výše uvedené tvrzení lze snadno dokázat. Pohybujme se po křivce IC (1. spotřebitel) z bodu X do bodu E (jak ukazuje šipka v grafu). Bod E je zajímavý tím, že se v něm křivka IC (1. spotřebitel) dotýká s jednou z IC popisujících preference 2. spotřebitele. Po celé trajektorii tohoto pohybu a samozřejmě i v bodě E je užitek 1. spotřebitele ze spotřeby obou výstupů stejný (protože se pohybujeme po indiferenční křivce), dochází jen ke změně kombinací výstupů, které jsou spotřebovávány. Vyčerpána je přitom vždy celá zásoba výstupů.
Pokud si představíme indiferenční křivku 2. spotřebitele, která prochází bodem X (v našem grafu ji nemáme zakreslenu, protože by tím byl obrázek příliš "přetížen", nepředstavuje však žádnou obtíž si ji domyslet), je zřejmé, že právě v bodě dotyku IC (2. spotřebitel) s příslušnou indiferenční křivkou popisující preference 2. spotřebitele (v grafu je zakreslena čárkovaně a není zvlášť označena) je při neměnné úrovni celkového užitku 1. spotřebitele dosaženo maxima užitku 2. spotřebitele. To je to, co jsme potřebovali dokázat, tj. že jakýkoli bod, který leží na průsečíku IC popisujících preference různých spotřebitelů nemůže být bodem optima a že všechny body na dotyku IC popisujících preference dvou spotřebitelů mohou být body optima. (Ke stejnému závěru bychom dospěli, pokud bychom se z bodu X posouvali příslušným směrem po křivce IC (2. spotřebitel); v tomto případě by zůstala zachována úroveň užitku 2. spotřebitele a zvyšoval by se užitek 1. spotřebitele.
Spojíme-li všechny body na dotyku IC dvou spotřebitelů získáme tzv. smluvní křivku (CC), která je v grafu vyznačena tučně. Název "smluvní" je odvozen od toho, že se statky (výstupy) mezi spotřebiteli směňují dobrovolně, jako výsledek vzájemně výhodné smlouvy.
Z výše řečeného vyplývá další významný závěr, který je čtvrtou podmínkou optimální alokace zdrojů: Pokud má být alokace (umístnění) výstupů v případě 2 výstupy, 2 spotřebitelé optimální, musí být mezní míra substituce (MRSC) výstupů, tj. poměr ve kterém může být nahrazen ve spotřebě každého spotřebitele jeden statek (výstup) druhým, aniž by se snížila úroveň celkového užitku spotřebitele, stejná.
(To je zřejmé mj. z toho, že v bodě dotyku mají IC obou spotřebitelů stejný sklon, přitom právě tento sklon vyjadřuje poměr, ve kterém lze zaměnit jeden spotřebovávaný statek za druhý, aniž by se snížil užitek ze spotřeby obou statků daným spotřebitelem.)
Optimum v případě: 2 vstupy, 2 výstupy, 2 spotřebitelé
Jedná se o nejrozvinutější schéma, které použijeme. Bývá též nazýváno schématem výrobně spotřební efektivnosti. Z toho, co potřebujeme, nezahrnuje v explicitní podobě pouze dva aspekty:
Optimalizaci rozdělení vstupů mezi dvě firmy.
Optimalizaci podílu obou firem na produkci dvou výstupů.
Obě tyto optimalizace však lze uvažovat relativně samostatně.
K vyjádření optima v tomto případě využijeme schématu složeného z krabicového (popisující optimum ve směně) a hranice produkčních možností:
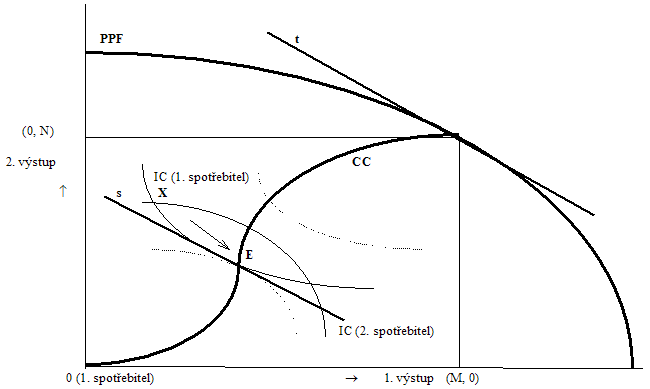
Z obrázku je zřejmé, že schéma vzniklo vložením krabicového diagramu popisujícího optimum ve směně, do schématu popisujícího hranici produkčních možností, která popisuje optimum ve výrobě.
Klíčovou roli v něm hrají tečny s a t. První je společnou tečnou dotýkajících se IC obou spotřebitelů (a vyjadřuje nám již známou skutečnost, že mezní míra substituce obou spotřebitelů musí být shodná). Druhá je tečnou PPF v bodě dotyku krabicového schématu popisujícího směnu. O ní víme, že vyjadřuje mezní míru transformace.
Tvrdíme, že schéma bude vyjadřovat paretooptimální situaci pouze a právě v tom případě, kdy obě tečny (s a t) budou rovnoběžné, tj, když mezní míra substituce obou spotřebitelů ve vztahu ke statkům, které spotřebovávají a které jsou výstupy výroby, bude rovna mezní míře transformace při výrobě těchto statků.
Výše řečené můžeme formulovat jako další závěr, který je pátou podmínkou optimální alokace zdrojů: Pokud má být alokace (umístnění) výstupů v případě 2 vstupy, 2 výstupy, 2 spotřebitelé optimální, musí být mezní míra substituce (MRSC) výstupů, tj. poměr ve kterém může být nahrazen ve spotřebě každého spotřebitele jeden statek (výstup) druhým, aniž by se snížila úroveň celkového užitku spotřebitele, stejná a současně se rovnat mezní míře transformace produktu (MRPT).
K výše řečenému několik poznámek:
Právě uvedené velmi významné tvrzení dokážeme v další části. Důkaz si totiž vyžaduje zavedení některých dalších pojmů.
Pokud výše uvedené tvrzení dokážeme, budeme moci zformulovat podmínky všeobecné rovnováhy.
O tom, ve kterém bodu smluvní křivky CC se transakce uskuteční, rozhoduje důchodová (příjmová) situace obou spotřebitelů, tj. to, jakými prostředky disponují. Otázku, odkud se příjmy spotřebitelů berou (čím je dána důchodová situace obou spotřebitel), model neřeší. (A ani to od něj nelze vyžadovat.)
Na poměrné důchodové situaci obou spotřebitelů ovšem závisí sklon tečny s. Při zlepšování poměrné důchodové situace 1. spotřebitele se bude bod transakce na smluvní křivce posouvat směrem od počátku souřadnic (k vyšší hladině jeho užitku). A naopak - při zlepšování poměrné důchodové situace 2. spotřebitele se bude bod transakce na smluvní křivce posouvat směrem k počátku souřadnic (směrem od druhého rohu diagonály).
Cena a její role při vytváření všeobecné rovnováhy
Doposud jsme se při hledání optima obešli bez explicitního bez pojmu "cena", resp. bez uvažování role cenového mechanismu. Vystačili jsme pouze s technickými parametry výroby a subjektivními preferencemi spotřebitelů.
Implicitně ovšem byl pojem ceny (resp. jejích některých atributů) v našich úvahách přítomen:
MRTP je svým způsobem "cena" obětované příležitosti v podobě množství jednoho z výstupů, kterého se musíme vzdát, pokud chceme zvýšit množství druhého výstupu.
MRSC představuje "cenu" v podobě množství jednoho výstupu, který se musí spotřebiteli zvýšit, aby byl ochoten obětovat určité množství druhého výstupu.
V obou případech porovnáváme množství dvou statků a to, co připomíná "cenu" má podobu poměru mezi dvěma statky (tj. podobu poměrné ceny).
O ceně jako takové ovšem můžeme hovořit teprve tehdy, když předpokládáme působení směnného, resp. tržního mechanismu. Cena jako taková je poměr, ve kterém se směňuje jeden statek za druhý. Přesněji - v tomto případě se jedná o poměrnou cenu. Pokud má jeden ze směňovaných statků specifickou podobu peněz, získáváme cenu v běžném smyslu slova.
Vraťme se nyní k našemu schématu výrobně spotřební efektivnosti a předpokládejme, že tečny s a t mají odlišný sklon.
Dále předpokládejme, že výrobci budou své výstupu dodávat na trh spotřebitelům za poměrnou cenu, která odpovídá sklonu tečny t.
(Další výklad provedeme až po prezentování schématu.)
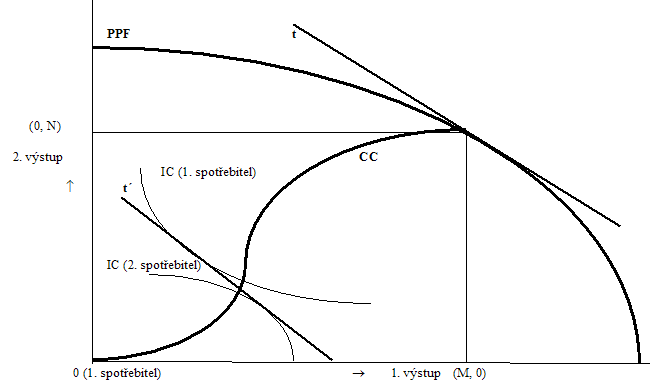
V tomto případě (při výše uvedené poměrné ceně) představuje přímka t´, která je rovnoběžné s tečnou t linii rozpočtového omezení obou spotřebitelů. Její umístění závisí na poměrné důchodové situaci obou spotřebitelů.
Bod dotyku t´ s příslušnou idndiferenční křivkou každého ze spotřebitelů představuje bod optima každého ze spotřebitelů představuje jeho bod optima jako spotřebitele.
Jak je zřejmé z obrázku, není daná situace paretooptimální. Příslušné body optima totiž neleží na CC a bylo by možné zvýšit užitek některého či obou spotřebitelů, např. (graficky vyjádřeno) posunem po IC každého z nich až do bodu, kde příslušná indiferenční křivka protíná CC.
Tohoto zvýšení užitku by bylo možné dosáhnout ještě jedním způsobem. Totiž tím, že by se (graficky vyjádřeno) posunul bod, v němž se dotýká tečně t hranice produkčních možností (křivky PPF), přitom tak, aby linie rozpočtu t´ splynula s tečnou s. (Tj. výrobci by volili jinou kombinaci výstupů.)
Dostáváme tak důležitý závěr, který představuje podstatnou část toho, co potřebujeme dokázat a co jsme si uvedli v předcházející části. Totiž že: Pokud má být alokace (umístnění) výstupů v případě 2 vstupy, 2 výstupy, 2 spotřebitelé optimální, musí být mezní míra substituce (MRSC) výstupů, tj. poměr ve kterém může být nahrazen ve spotřebě každého spotřebitele jeden statek (výstup) druhým, aniž by se snížila úroveň celkového užitku spotřebitele, stejná, přitom stejná s mezní mírou transformace produktu (MRPT).
Zbývá ještě dokázat, že pokud budou výrobci nabízet své výstupy za jinou poměrnou cenu než odpovídá sklonu tečny t, situace rovněž nebude paretooptimální. K tomu použijeme následující schéma:
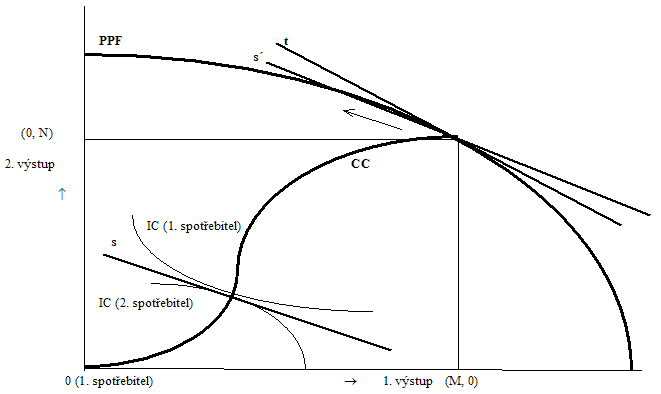
Nechť nyní výrobci dodávají své výrobky na trh za poměrnou cenu, která je vyjádřena sklonem přímky s´. Ta je rovnoběžná s tečnou s, která je tak současně linií rozpočtového omezení spotřebitelů. Problém, se kterým jsme se setkali v přecházejícím případě, nevzniká.
Vzniká ovšem jiný problém. Posuneme-li se po hranici produkčních možností ve směru šipky, zvýší se příjem výrobců. To znamená, že ani v tomto případě nemohla být situace paretooptimální. Tím jsme vlastně dokázali to, co jsme potřebovali dokázat, tj. že situace je paretooptimální tehdy a právě tehdy, když jsou tečny s a t rovnoběžné.
Poznámka:
Pokud bychom měli konkrétní zadání, nebyla by konkrétní cesta nalezení optima, které by splňovalo všechny optimalizační podmínky (tj. optimalizace využití vstupů v každé výrobě, optimalizace rozdělení vstupů mezi dvě výroby, optimalizace složení výstupů a optimalizace směny), jednoduchá.
To je dáno tím, že všechny optimalizace musejí být provedeny současně, resp. každá dílčí optimalizace okamžitě mění podmínky pro všechny ostatní. Bylo by možné postupovat např. cestou postupného přiblížení (iterace). Výsledek ovšem může být velmi závislý na počátečních podmínkách.
Nám však nejde o číselné řešení. Smysl výše uvedeného je jiný. O tom si řekneme něco více poté, co zformulujeme podmínky všeobecné rovnováhy.
Mj. - ukazuje se, že reálně působící tržní mechanismus se v podstatě chová jako iterativní mechanismus a jím generované tržní ceny poskytují informace, které orientují ekonomické subjekty při zlepšování jejich užitku.
Podmínky všeobecné rovnováhy
Na základě výše uvedeného lze formulovat podmínky, které musí být splněny, pokud má být dosažena všeobecná rovnováha. A to jak v námi uvažovaném případě 2 vstupů, 2 firem, 2 výstupů, 2 spotřebitelů, tak i v případě libovolného počtu vstupů, firem, výstupů, spotřebitelů:
Mezní míra technické substituce (každého) jednoho vstupu za druhý musí být stejná pro oba (všechny) výstupy.
Mezní míra substituce ve spotřebě (každého) jednoho výstupu za druhý musí být stejná pro všechny oba (všechny) spotřebitele.
Společná míra substituce ve spotřebě se musí rovnat společné míře transformace pro oba (všechny) výstupy.
Za těchto podmínek současně platí, že poměrná cena výstupů (poměr ceny jednoho statku ke druhému) se rovná mezní míře substituce ve spotřebě a mezní míře transformace při jejich výrobě.
(Tj. - a to je rovněž důležitý závěr - cena není vnější veličinou, ale je výsledkem utváření všeobecné rovnováhy, tj. - z hlediska modelu - vnější, tj. endogenní veličinou. Dlužno zdůraznit, že na rozdíl od důchodové situace spotřebitelů, která je ve vztahu k modelu vnější, tj. exogenní veličinou.)
Poznámka:
Existuje rozšířený model, který i důchodovou situaci všech subjektů, které se podílejí na utváření všeobecné rovnováhy, odvodil jako endogenní veličinu. Takový model lze vytvořit na základě pojetí spotřeby jako produktivního fenoménu, přičemž výsledkem spotřeby je vytváření investičních příležitostí, kterými disponují jednotlivé ekonomické subjekty. Ukážeme si ho v příslušné části tohoto textu.
Význam modelu všeobecné rovnováhy
Model všeobecné rovnováhy je nepochybně elegantním (a ne triviálním) výsledkem ekonomického bádání. O jeho praktickém přínosu či praktické aplikovatelnosti se vedou spory. Problém je totiž v tom, že reálný ekonomický systém nevede k jejímu vytváření a že všeobecná rovnováha není ani "ekonomickým ideálem". Reálný ekonomický systém je dynamický a inovace (které do něj prostřednictvím lidských schopností vstupu), ale i řada dalších vlivů jej neustále vyvádějí z rovnováhy (a to dříve, než by ji bylo možné dosáhnout).
Přesto - či právě proto - má model všeobecné rovnováhy značnou vypovídací schopnost. Musíme si ovšem uvědomit, že v každém okamžiku působí dva protichůdné vlivy:
Adaptační chování ekonomických subjektů na základě informací zprostředkovaných tržních mechanismem a jím generovanou cenou statků, které iterativním způsobem směruje ekonomický systém k rovnováze.
Inovační chování ekonomických subjektů (které je také zprostředkováno informacemi poskytovanými cenami), které vyvádí ekonomický systém z rovnováhy (mění podmínky rovnováhy).
Kromě toho v reálném ekonomickém systému působí i vlivy, kterými se některé ekonomické subjekty snaží zlepšit svůj užitek blokováním procesů vedoucích k rovnováze i blokujících inovační chování (tak je tomu zejména v případě působení některých typů monopolů).
Navíc v reálném ekonomickém systému hraje určitou roli stát (případně i další subjekty veřejné volby). Těmito otázkami se budeme zabývat v dalším oddílu.
Představa o všeobecné rovnováze je při pohledu na reálný ekonomický systém velmi důležitá. (Máme samozřejmě na mysli představu, která vyplývá z pochopení jejího modelu a schopnosti správně jej používat jako prizmatu, přes které se na ekonomickou realitu díváme.) Umožňuje totiž mj. následující:
Vidět adaptační procesy směřující k obnovování rovnováhy.
Identifikovat roli inovačních procesů.
Odhalit různé překážky jak adaptačního, tak i inovačního chování (podstatné či v daných podmínkách určující vlivy, které v dané situaci působí proti efektivnosti ekonomického systému).
Identifikovat případy tzv. tržních selhání či tzv. nedokonalostí trhu.
Hledat cesty tzv. paretovských zlepšení v případech kdy z různých důvodů dochází k selhání trhu nebo když proces optimalizace naráží na nedostatky (nerozvinutost) trhu.