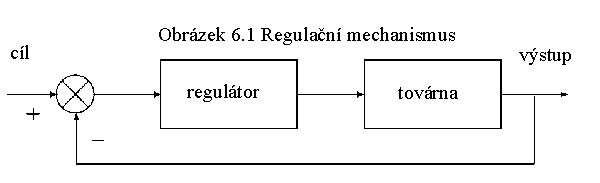
V kapitole 4 jsme představili plánování jako případ regulace pomocí zpětné vazby. Rekapitulací této základní myšlenky je obrázek 6.1. Tuto obecnou koncepci lze nyní rozpracovat tak, aby vzala v úvahu konkrétní vývody týkající se socialistického plánování, k nimž jsme dosud dospěli.
Jak jsme viděli, strategické plánování se zabývá celkovou podobou odvětvové struktury dané ekonomiky. Námětem této kapitoly bude detailní plánování, které řeší otázku, jaké množství každého jednotlivého produktu je třeba vyrobit, aby byly splněny obecné cíle vyplývající ze struktury. Strategický plán například stanoví, že se má na výrobu elektronického spotřebního zboží alokovat 7 procent národního důchodu. Detailní plán musí říci, kolik to bude znamenat televizních přijímačů podle jednotlivých modelů, kolik jednotlivých typů zesilovačů atd. Aby byly dosaženy tyto cíle celkové produkce, plán musí také specifikovat počty všech typů součástek potřebných k sestavení zesilovačů a televizorů: 500 000 barevných obrazovek s diagonálou 14”, 300 000 s diagonálou 20”, 12,5 milionů 10-mikrofaradových keramických kondenzátorů atd.
Obrázek 6.2 znázorňuje vstupy do detailního plánování. Blok „simulace a rozpisy” zahrnuje sestavení podrobného modelu provozu celé ekonomiky, aby bylo možné předpovědět, kolik polotovarových vstupů bude třeba pro výrobu požadované kombinace konečných výstupů. Marketing - který vstupuje do detailního plánování nepřímo - poskytuje zpětné informace o tom, zdali je cena, kterou jsou lidé ochotni zaplatit za daný produkt dostatečně vysoká na to, aby byl produkt nadále začleňován do plánu. Pokud lidé nejsou ochotni zaplatit ve formě pracovní doby tolik, kolik pracovní doby bylo třeba na jeho výrobu, pak je třeba výrobu tohoto konkrétního produktu omezit nebo ukončit a přesunout zdroje na něco jiného. Podrobnosti této námi navrhované zpětné marketingové vazby popíšeme v kapitole 8; pro tuto chvíli se soustředíme na simulaci a alokaci.
V kapitole 3 jsme zavedli tabulky vstupů a výstupů v souvislosti s výpočtem celkového pracovního obsahu jednotlivých komodit. Tato metoda znázornění ekonomických skutečností je velmi vhodná také pro formulaci a pochopení problémů detailního plánování. Jeden možný příklad takové tabulky vstupů a výstupů je uveden v tabulce 6.1. Čtenář se také může vrátit k příkladu znázorněnému v tabulce 3.2. Připomeňme, že tabulka neboli matice vstupů a výstupů zaznamenává tok produktů z každého jednotlivého odvětví ekonomiky do všech ostatních odvětví. Každé odvětví v ní vystupuje dvakrát, je mu přidělen jeden řádek a odpovídající sloupec. V podobě, jakou používáme zde, jsou v řádku daného odvětví uvedena množství produktů daného odvětví, která plynou jako vstupy do všech odvětví. Jestliže se např. řádek 1 týká ropného průmyslu, čísla v tomto řádku představují množství ropy dodaná samotnému ropnému průmyslu, pak výrobě elektřiny, výrobě nákladních automobilů atd. Každý sloupec pak udává kvantity produktů, které dané odvětví potřebuje jako své vstupy. Např. jestliže sloupec 3 představuje výrobu nákladních automobilů, najdeme v tomto sloupci odshora dolů množství ropy, elektřiny atd., které je k výrobě nákladních automobilů zapotřebí.
Tabulka 6.1: část tabulky vstupů a výstupů
|
ropa |
elektřina |
nákladní automobily |
atd. |
|
| ropa |
1 000 |
50 000 |
800 |
… |
| elektřina |
50 |
20 |
40 |
… |
| nákladní automobily |
30 |
10 |
20 |
… |
| atd. |
… |
… |
… |
… |
Pro pochopení toho, co se zde děje, se bude hodit něco základních termínů. Především je to hrubý objem výroby daného odvětví, což je celkový objem výroby odvětví bez ohledu na její následné využití. Hrubý objem výroby se dělí na objem výroby polotovarů a finální neboli čistý objem výroby. Objem výroby polotovarů je ta část celkového produktu odvětví, která je určena pro „spotřebování” uvnitř samotného systému výroby (např. uhlí používané v ocelářství, nebo ocel používaná v odvětví výroby osobních počítačů). Finální neboli čistý objem výroby je zbývající část produktu, která je určena ke koncovému použití (buď ke spotřebě, ať individuální nebo kolektivní, nebo jako čisté investice určené na rozšíření produktivní základny ekonomiky).
Některé produkty jsou víceméně čisté polotovary. Tak například - snad s výjimkou malého počtu kutilů - spotřebitelé vůbec nemají zájem o ocelový plech, takže prakticky celá jeho produkce bude vystupovat jako polotovar vstupující do produkčního procesu v různých odvětvích. Na druhé straně některé produkty jsou čisté finální statky, které nemají jako polotovary využití (žádné odvětví nepoužívá jako vstup balíčky cigaret). Některé produkty se však používají jako polotovary i jako finální statky. Zemní plyn se používá v domácnostech k vaření a vytápění, ale v řadě odvětví je také výrobním vstupem.
Důležitý je ještě jeden termín: technický součinitel dané uspořádané dvojice odvětví, který říká, jaká část produkce jednoho odvětví je zapotřebí (přímo) k výrobě jedné jednotky produkce druhého odvětví. Například jestliže je na výrobu jednoho jízdního kola třeba 10 kilogramů ocelových trubek, potom technický koeficient dvojice (ocelové trubky, jízdní kola) je 10, pokud se ocel měří na kilogramy, nebo 0,01, pokud se měří na tuny. Všimněme si, že celkový požadavek na vstup ocelových trubek lze zjistit vynásobením celkového objemu výroby kol příslušným technickým koeficientem. Při koeficientu 0,01 by výroba 2000 kol vyžadovala 2000 x 0,01 = 20 tun ocelových trubek.
Teď už můžeme začít uvažovat o struktuře problémů, které stojí před plánovači socialistické ekonomiky. To, o co lidé mají koneckonců zájem, je hromada finálních statků, které produkuje ekonomika. Předpokládejme, že máme pro tyto statky určen soubor cílových hodnot.[24] Splnění těchto cílů vyžaduje, aby byla vyrobena potřebná množství polotovarů. Výrobci osobních počítačů mohou dodat požadovaná množství a typy počítačů pouze tehdy, když od svých dodavatelů dostanou potřebné množství plastických hmot, oceli, křemíku atd., což ale znamená, že i tito dodavatelé musí dostat polotovary, které sami potřebují atd., takže všichni jsou součástí velmi složité sítě vzájemných závislostí.
Problém tedy zní: vyjdeme-li ze seznamu požadovaných finálních výstupů, jak vypočítat hrubá množství všemožných produktů potřebných k dosažení těchto zadaných finálních hodnot? V principu lze dojít k odpovědi přímo, a to následujícím způsobem. (Čtenáři, kteří nemají v oblibě matematické vzorce, mohou přeskočit pár následujících odstavců a přejít hned k závěru, používáme však jen tu nejjednodušší algebru.) Uvažujme o jednoduchém systému, který se skládá jen ze dvou odvětví. Nechť G označuje hrubý objem výroby, I objem vyrobených polotovarů, F finální objem výroby. Dolní indexy označují obory 1 a 2. Protože hrubý objem výroby se rovná součtu objemu výroby polotovarů a finálního objemu výroby, můžeme znázornit naši drobnou ekonomiku dvěma rovnicemi, jednou pro každé odvětví.
G1 = I11 + I12 + F1
G2 = I21 + I22 + F2
První ze dvou dolních indexů u objemů výroby polotovarů (I) označuje zdroj produktu, druhý jeho určení, takže např. I12 označuje množství produktů odvětví 1, které budou použity v odvětví 2. Vyjádřeno česky, první rovnice říká, že hrubý objem výroby prvního odvětví se skládá ze tří částí: za prvé z objemu výroby polotovarů odvětví 1 spotřebovaného v tomtéž odvětví (tak jako např. ropný průmysl spotřebuje také něco ropy; u odvětví, které svůj vlastní produkt nepotřebují, bude tento člen rovný nule); za druhé z objemu výroby polotovarů odvětví 1, který potřebuje odvětví 2; a za třetí z finálního neboli čistého objemu výroby produktu číslo 1.
Nyní proveďme následující jednoduchou úpravu: všechny hodnoty objemu výroby polotovarů (I) přepíšeme jako součiny hrubého objemu výroby (G) a příslušného technického koeficientu. Jestliže technické koeficienty označíme písmenem a , dostaneme následující:
G1 = a11G1 + a12G2
+ F1
G2 = a21G1 + a22G2
+ F2
Řešení problému je už teď nasnadě: záměnou všech I za násobky a a G jsme jej redukovali na řešení dvou rovnic o dvou neznámých, kterými jsou hrubé objemy výroby obou odvětví. Pomocí jednoduchých, ale pracných algebraických výpočtů bychom pak získali žádaný výsledek: hrubé objemy výroby pro každé odvětví jako funkce pouze finálních objemů výroby a technických koeficientů. Jakmile jsou pak k dispozici hrubé objemy výroby, lze z nich snadno vypočítat i objemy výroby polotovarů vstupujících do každého odvětví - jako v našem příkladu s jízdními koly.[25]
Matematická stránka problému je dnes jasná díky pionýrským pracím Vasilije Leontieva a Johna von Neumanna zveřejněným ve 30. a 40. letech 20. století. Řešení není příliš obtížné, pokud je systém dostatečně malý. Ale když máme co dělat s ekonomikou jako celkem, jediný způsob jak dospět k „malému” systému je vyjádřit jej pomocí vysoce agregovaných veličin. Řádky a sloupce naší tabulky mohou představovat dejme tomu „spotřební elektroniku”, „motorová vozidla”, „ropu a plyn” a tak dále. Pro některé účely je tento postup přijatelný, pro praktické socialistické plánování však nestačí. Pokud mají plánovači přijít s návrhem dokumentu, který by byl efektivní směrnicí pro výrobu zajišťující správnou provázanost všech ekonomických činností, musí být schopni specifikovat vstupy a výstupy přesně a do detailu. V takovém případě ovšem tabulka vstupů a výstupů nabude kolosálních rozměrů s miliony řádků a sloupců a tedy tisíci miliard technických koeficientů. Řešení výsledného sytému lineárních rovnic pak není zrovna triviální úkol. Navíc ještě před zahájením výpočtů je třeba shromáždit ohromné množství podrobných informací (např. technických koeficientů).
Získávání informací a jejich matematické zpracování: obě tyto otázky jsou důležité. Začneme zkoumáním výpočetního procesu, přičemž předpokládáme, že potřebné údaje jsou „dány” (což je oblíbené slůvko ekonomů); v kapitole 9 se pak vrátíme k problému získávání údajů.
Matematické problémy, které před námi vyvstávají, jsou v podstatě tytéž, jako u výpočtu pracovních hodnot, kterým jsme se zabývali v kapitole 3. V zásadě lze úkol řešit přímo pomocí Gaussovy eliminační metody, ale jak jsme viděli v kapitole 3, pro příliš velké systémy je tato cesta z praktických důvodů neschůdná. Jako u výpočtu pracovních hodnot lze poustupovat tak, že využijeme skutečnost, že matice vstupů a výstupů neboli naše „tabulka” bude obsazena jen řídce. Vzhledem k tomu, že tabulka bude mít při rozepsání na podrobné položky spoustu nulových polí (zubní pasta se nepoužívá k výrobě salámu, řezivo se nepoužívá k výrobě brýlí atd.), je lepší popsat podmínky výroby pomocí navzájem propojených dílčích tabulek a hledat řešení iterací.
Obě hlavní iterační techniky, které jsou k dispozici (Jacobiho a Gaussova-Seidelova metoda) vycházejí ze vstupních dat ve formě propojených dílčích seznamů. K výsledku nedospívají přímo, ale řadou postupných přiblížení. V případě aplikace na ekonomické vstupy a výstupy lze dokázat, že pokud má systém jediné řešení - což lze v zásadě zjistit přímo -, pak zmíněné iterační metody budou dávat výsledky, které budou k tomuto řešení konvergovat (Varga, Richard S. Matrix Iterative Analysis, Englewood Cliffs, NJ: Prentice-Hall, 1962).
Jak funguje iterační metoda v této aplikaci lze vysvětlit poměrně snadno. Požadovaná vstupní data tvoří (i) seznam požadovaných finálních výstupů, (ii) technické koeficienty (s nenulovou hodnotou) a (iii) nějaký počáteční odhad požadovaného hrubého objemu výroby každého produktu. Tyto výchozí hodnoty hrubých objemů výroby se pak vynásobí technickými koeficienty a stanoví se tak množství všech produktů, které jsou potřebné jako vstupy. Na tomto základě se vypočítá nový soubor hodnot hrubých objemů výroby. Tento soubor se použije jako vstup pro druhé kolo výpočtu a tak dále. Pokud algoritmus konverguje (podmínkou toho je především, aby systém měl jediné řešení), potom se po chvíli začnou změny hodnot hrubých objemů výroby kolo od kola zmenšovat. Algoritmus skončí tehdy, když tyto změny klesnou pod nějakou předem zadanou „malou” veličinu.
Volba výchozích hodnot hrubých objemů výroby nehraje zásadní úlohu, protože konvergenční vlastnosti algoritmu nezávisí na počátečních podmínkách: pokud se „ujmou” některé z výchozích hodnot, učiní totéž i ostatní (opět viz Varga, citované dílo). Nicméně konvergence bude rychlejší, pokud jsou počáteční odhady poměrně blízké správným hodnotám. Jestliže jsou k dispozici předchozí zkušenosti, mohou se o ně plánovači při stanovení přibližné velikosti výchozích hodnot opírat.
Čas potřebný na výpočet Jacobiho iterační metodou je řádově dán vzájemným násobkem počtu výstupů, průměrného počtu jednotlivých přímých vstupů do každého výrobního procesu a počtu iteračních kol potřebných k dosažení uspokojivého výsledku. Máme-li dejme tomu 10 milionů produktů, má-li každý z nich v průměru 200 přímých vstupů a jestliže je zapotřebí 100 iterací, pak je třeba provést 2x1011 výpočtů. Předpokládejme, že každý výpočet vyžaduje 10 počítačových instrukcí. V takovém případě máme celkem 2x1012 instrukcí a počítač s rychlostí jedné miliardy instrukcí za vteřinu zvládne tuto práci za 2x103 vteřin, tj. za něco víc než půlhodinu.
V tomto okamžiku se nabízejí dvě otázky, týkající se vztahu mezi našimi dosavadními úvahami v této kapitole a zkušenostmi z plánování v Sovětském svazu. Za prvé se lze zeptat: jestliže důsledné detailní plánování vyžaduje tak rozsáhlé a složité výpočty, jak je vůbec mohli Sověti zvládnout, když ještě neexistovaly vysokorychlostní počítače?
Je opravdu pozoruhodné, že Sověti ve 30. letech 20. století, kdy ještě vůbec nebyly počítače, dosáhli takových úspěchů v budování své základny těžkého průmyslu s použitím metod centrálního plánování. Ekonomika byla tehdy samozřejmě technicky mnohem méně složitá a v plánech byl zadán poměrně malý počet klíčových úkolů. Přesto existuje spousta informací o hrubých disproporcích mezi nabídkou a poptávku, k nimž docházelo v průběhu prvních pětiletek. Obrovský nárůst vstupů pracovní síly i materiálů však umožnil splnění těchto klíčových úkolů přes uvedené disproporce.
Kromě toho je třeba zdůraznit, že první sovětské plány se nesestavovaly způsobem, jaký jsme popsali v této kapitole. Propracovat se důsledně a do podrobností od požadovaných finálních objemů výroby až k hrubým objemům výroby jednotlivých produktů byl úkol, který naprosto přesahoval možnosti tehdejšího státního plánovacího úřadu, Gosplanu. Namísto toho plánovači často vycházeli z cílů zadávaných ve formě hrubých objemů výroby: tolik a tolik tun oceli do roku 1930, tolik a tolik do roku 1935 a tak dále. Tato prvotní zkušenost měla podle všeho nepříznivý vliv na ekonomické mechanismy pozdějších let. Dala vzniknout jakémusi „produkcionismu", při němž se dosahování rekordních objemů výroby klíčových průmyslových polotovarů začalo považovat za cíl samo o sobě. Ve skutečnosti je z pohledu vazeb mezi vstupy a výstupy žádoucí, aby se polotovary co nejvíc šetřilo. Cílem by mělo být vyrábět minimální množství uhlí, oceli, cementu atd. odpovídající požadovaným objemům finálních výstupů.
Druhá otázka vyvstávající v této souvislosti je v jistém smyslu opakem první: jestliže jsou výše probírané matematické a výpočetní techniky tak dobře známé, proč se sovětským plánovačům nedařilo o moc lépe v polovině 80. let, když už byly dostupné rychlé počítače?
Částečnou odpověď jsme dali, když jsme pojednávali o první z těchto dvou otázek. Nevyhnutelně značně hrubé plánovací metody 30. let poznamenaly pozdější vývoj systému. Vzhledem ke specifické ideologické skleróze posledních let Stalinovy éry - přerušené Chruščovovou „oblevou”, ale recidivující za Brežněva - se na nové přístupy k plánování obecně hledělo s podezřením. V literatuře o sovětské ekonomice najdeme náznaky, že samotná myšlenka plánování vycházejícího z cílů stanovených pro finální objemy výroby (přístup, který jsme zdůvodňovali v této kapitole) byla považována oficiálními strážci pravověrnosti za poněkud „buržoasní”.
Navíc zájem o nové metody plánování pomocí počítačů v SSSR přišel v nevhodný čas z hlediska reálných technologických možností. Počítačové systémy, které měl SSSR k dispozici v 60. a dokonce i 70. letech (kdy bylo zdokonalení plánování velmi živou otázkou), byly ve srovnání s nynějším západním standardem velmi primitivní. Sovětští ekonomové si byli dobře vědomi potenciálních přínosů, které mohlo znamenat důsledné zavádění techniky vstupů a výstupů, ale jim přístupné počítače umožňovaly pouze analýzu „malých” vysoce agregovaných systémů vstupů a výstupů. I když se daly do určité míry využít při pokusech o regionální plánování (při výzkumu vzájemných závislostí regionů SSSR), nedaly se použít pro rutinní detailní plánování. Analýza vstupů a výstupů tak zůstala převážně akademickou záležitostí a celkový vliv počítačů na sovětský plánovací systém zklamal předchozí očekávání.[26]
Je důležité připomenout, že nedostupnost superrychlých ústředních počítačů nebyla jedinou a dokonce ani nejdůležitější překážkou. Jak jsme ukázali v kapitole 3 v souvislosti s výpočtem pracovních hodnot, stejných výsledků by bylo možné dosáhnout pomocí rozsáhlé distribuované sítě mnohem skromnějších osobních počítačů, navzájem propojených telekomunikačním systémem pokrývajícím celou ekonomiku. V době, kdy sovětští ekonomové seriózně uvažovali o zdokonalení vlastního plánovacího systému, bylo ovšem i podobné vybavení nedostupné. Levné osobní počítače se objevily relativně nedávno, a kromě toho telekomunikační systém SSSR je nechvalně znám svou zaostalostí (jak ví každý, kdo se někdy pokusil dovolat z Moskvy do Leningradu).
Dále, jak uvidíme v kapitole 9, účinné detailní plánování vyžaduje standardizovaný systém identifikace produktů, který také vyžaduje složité počítačové databáze. V SSSR plánovači nadále pracovali se systémem tzv. „materiálových bilancí”. Tento systém, založený na sestavování „bilancí” pro jednotlivé produkty udávajících zdroje potřebné na jejich výrobu a jejich plánované využití, je pouze jakousi hrubou aproximací metody vstupů a výstupů. Plánovači nejenže nebyli schopni efektivně vypočítat vzájemné interakce mezi těmito bilancemi, ale neúplná a rozporná byla i klasifikace produktů.
Zde je třeba uvést také jednu politickou okolnost. Námi navrhovaný způsob plánování absolutně vyžaduje svobodný tok informací a všeobecný přístup k počítačovým systémům, což bylo v SSSR za Brežněva nemožné z politických důvodů. Z obavy před šířením politického disentu by přísně kontrolován dokonce i přístup ke kopírkám.
Závěrem nutno konstatovat, že počítače samozřejmě nejsou všelékem. Aby využití mimořádně výkonných počítačů přineslo v SSSR nějaké podstatnější výsledky, musela by se nejdřív řešit řada dalších problémů, kterými trpěl mechanismus plánování ekonomiky. (Jeden příklad: iracionální a napolo zkamenělý systém tvorby cen, který držel ceny řady zboží na úrovni zaručující jejich nedostatek a vytváření front.)
Efektivní detailní plánování komplexní ekonomiky podle všeho předpokládá takovou úroveň počítačové a telekomunikační techniky, jaká byla na Západě k dispozici asi od poloviny 80. let. Do té doby se už ovšem ideologické klima v SSSR podstatně změnilo ve prospěch „reforem” orientovaných na trh. Zdá se, že sovětští ekonomové - nebo v každém případě ti, kterým za Gorbačova naslouchalo politické vedení - neměli velký zájem o vyvíjení algoritmů a počítačových systémů, o kterých jsme zde hovořili. Zřejmě už ztratili víru v potenciál efektivního plánování, což možná byla zčásti reakce na dřívější předčasné a neúměrné vychvalování předností počítačů, zčásti pak odezva na západní trend příznivý tržní ekonomice.
Abychom se vrátili k hlavní linii naší argumentace, zopakujme naše tvrzení, že dnes je pro plánovací instituci docela schůdným úkolem vyjít ze seznamu úkolů pro finální výrobu a propracovat se odtud zpět k seznamu hrubých objemů výroby, které povedou k vyváženému plánu, a to i v případě, že tabulka vstupů a výstupů popisuje vzájemné vztahy mezi odvětvími až do nejmenších podrobností. Tím ovšem výpočty potřebné pro detailní plánování nekončí. Výrobě požadovaných množství všech produktů podle požadavků vyplývajících z výpočtů hrubých objemů výroby totiž mohou bránit „vnější” překážky, vyplývající z omezenosti zásob výrobních prostředků a disponibilního objemu pracovní doby.
Plánovači například vypočítají, že splnění úkolů plánu vyžaduje, aby se vyrobilo x terakilowatthodin elektřiny. Vybilancováním systému vstupů a výstupů lze zajistit pro tuto výrobu dostatečné dodávky ropy, uhlí a uranu, ale co když nebude k dispozici dostatečná kapacita elektráren? Schopnost ekonomiky vyprodukovat něco za určité období je omezena tím, zda je k dispozici dostatečné množství trvalých kapitálových statků, jejichž vytváření trvá dlouhou dobu. A pak jsou zde pracovní síly: je jich k dispozici dostatečné množství na splnění všech plánovaných úkolů hrubého objemu výroby?
Tyto otázky lze zodpovědět velmi rychle, jakmile jsou známy číselné hodnoty hrubých objemů výroby. Plánovací systém může předat tyto požadavky jednotlivým odvětvím, a ty pomocí své výpočetní techniky (což nemusí být zrovna superrychlé počítače) určí, jak velký objem výrobních prostředků a pracovní doby potřebují ke splnění úkolů plánu, přičemž použijí vlastní údaje o objemu výrobních prostředků na jednotku produkce a koeficientech pracovní doby ve svém sektoru. Tyto požadavky jednotlivých odvětví pak lze zpětně zadat do centrálních počítačů, vypočítat souhrnné hodnoty a porovnat je s centrální evidencí výrobních prostředků různých typů a také s centrální evidencí pracovních sil.
Pokud nevzniknou úzké profily - tj. pokud odvětví nepožadují větší množství různých typů výrobních prostředků a větší množství pracovní doby, než jaké má k dispozici ekonomika jako celek, je všechno v pořádku. Je ovšem třeba připomenout, že i když v celkovém souhrnu úzké profily nevzniknou, může být nutná realokace zdrojů mezi jednotlivými odvětvími a centrální plánovací instituce pak musí tyto přesuny optimalizovat a vydat příslušné instrukce. Pokud ale vzniknou úzké profily v celkových kapacitách, je třeba nějak upravit plán. Není možné dosáhnout původně požadované finální objemy výroby (pokud se nějakým způsobem nepodaří změkčit „vnější” omezení) a plánovači musí tedy znovu přemýšlet. Lze omezit ty úkoly finálních objemů výroby, které mají nejnižší sociální prioritu a celý výpočet zopakovat znovu. Jelikož celý proces bude pravděpodobně trvat několik hodin, v nejhorším případě několik dnů, lze takových opakovaných výpočtů udělat celou řadu a přitom dodržet rozumně stanovený časový termín pro sestavení plánu.
Jaký skutečný význam má tato poslední okolnost, tj. existence úzkých profilů výroby, které nejsou zohledněny v systému toků vstupů a výstupů, podstatně závisí na délce období, na které se plánuje. Jestliže jde o plán na dostatečně dlouhé období, nebudou úzké profily takovým problémem. Požadují-li se větší kapacity pro výrobu elektřiny, lze je v průběhu tohoto období vybudovat. V limitním případě pak budou jedinými „vnějšími” omezeními ekonomického systému vstupů a výstupů disponibilní množství pracovní doby a dostupnost neobnovitelných přírodních zdrojů. V takovém případě by přizpůsobení úkolů finálních objemů výroby vnějším omezením mělo být poměrně jednoduchou záležitostí. Ovšem naopak čím kratší je plánovací období, tím jsou úzké profily závažnější. Za úzký profil je třeba považovat každý výrobní prostředek, jehož výstavba nebo pořízení trvá delší dobu, než na jakou se plánuje; pokud se plánuje na velmi krátké období, začínají být důležité i zásoby materiálu. Jeden z autorů této práce zkoumal počítačový algoritmus schopný vybilancovat plán i v takové situaci. Algoritmus se ovšem značně odlišoval od výše popisovaného standardního přístupu založeném na vstupech a výstupech. Teoretický základ tohoto algoritmu představíme v následující části současně s konkrétním příkladem jeho aplikace.
Předpokládejme, že vyjdeme ze seznamu požadovaných ročních objemů výroby pro 100 000 různých spotřebních statků. Tyto úkoly mohou být konzervativní a část zdrojů pak zůstane nevyužita, nebo mohou být nadměrné a přesahovat možnosti dané současnými zdroji. Chceme zjistit, jak se mají zvyšovat či snižovat úkoly plánu v zájmu efektivního využití zdrojů, včetně zásob různého strojního vybavení existujících v ekonomice jako celku. Je málo pravděpodobné, že toho lze dosáhnout jednotnou změnou kvót všech spotřebních statků o x procent. Kvóty jednotlivých statků bude třeba upravovat směrem nahoru i dolů o různé hodnoty.
Jestliže máme k dispozici pouze omezené počty ovcí a volnou kapacitu v chemickém průmyslu, potřebujeme vědět, co to bude znamenat pro kvóty svetrů z vlny a akrylu. Je třeba snížit plán výroby vlněných oděvních součástí? A co to znamená pro výrobu akrylových? Kolik pletacích strojů je třeba převést ze zpracování vlny na akryl?
Předpokládejme, že volné pletací stroje lze převést na výrobu kteréhokoli z tisíce typů pleteného zboží. Veškerou volnou kapacitu lze nasadit na zvýšení výroby konkrétního druhu svetrů v zářivě modré barvě s růžovým nápisem „St Tropez Sport” přes prsa, ale není jisté, jestli se takové řešení bude líbit spotřebitelům. Je třeba mít soubor pravidel, podle nichž budou počítače schopny rozhodnout, jak mají s určitou pravděpodobností vypadat rozumné úpravy plánu s ohledem na omezenost zdrojů. Vyvinuli jsme počítačový program, který dělá takové úpravy na základě ekonomického principu klesající marginální užitečnosti. Podrobný popis algoritmu lze najít ve stati W. Paula Cockshotta „Application of artificial intelligence techniques to economic planning”, Future Computing Systems,, vol 2, 1990, 429-43.
Algoritmus využívá techniky vyvinuté pro simulaci neuronových sítí (což je jeden z dílčích oborů výzkumu umělé inteligence). Výzkumníci pracující v této oblasti přišli s návrhem, aby se neuronové systémy analyzovaly pomocí pojmů termodynamiky. Nervový systém se skládá z obrovského množství navzájem volně spojených prvků a jako takový patří do abstraktní kategorie problémů, kterými se zabývá statistická mechanika. Ukázalo se, že u neuronových modelů lze dobře využít termodynamické pojmy jako je energie, entropie a relaxace. Každý neuron podobně jako každý atom látky v pevném skupenství je ve spojení s určitou podmnožinou celkového množství neuronů a na tuto podmnožinu reaguje. V obou případech máme co dělat s obrovskými množinami, které se mění podle stochastických zákonů[27] pod účinkem lokálních interakcí. Pro neuronovou síť lze definovat vhodnou analogii pojmu energie - ta zhruba řečeno udává, do jaké míry se chování sítě blíží žádoucímu chování. Lze ukázat, že pokud se do chování neuronové sítě zavede určitá počítačová analogie teploty, potom lze pomocí relaxačního procesu přimět síť, aby se stabilizovala v blízkosti žádoucího vzorce chování.
Rozvíjíme-li tuto analogii dále, lze neuronové sítě a krystaly přirovnat na určité úrovni abstrakce k ekonomice. V ekonomice jsou jednotlivá odvětví navzájem propojena lokálními interakcemi. Namísto synaptických spojů nebo elektrostatických sil máme v tomto případě vztahy mezi dodavateli a uživateli, ale je zde určitá abstraktní podobnost.
Všimněme si podobnosti mezi neuronovou sítí na obrázku 6.3 a maticí vstupů a výstupů. Svislé šipky v diagramu představují výstupy z nervových buněk na pravé straně. Synapse přivádějí vstupy do buněk, které jsou představovány řádky. Řádky fungují tak, že sčítají úroveň vzruchů na svých vstupech. Úroveň vzruchů na vstupech ale zase určuje úroveň výstupů na axonech. Můžeme vytvořit analogii svislých šipek se sloupci tabulky vstupů a výstupů, které představují úroveň aktivity daného ekonomického odvětví. Označme synapse symbolem Sij, kde i označuje řádky a j svislé šipky. Síla vazby na synapsi Sij představuje objem výstupů i-tého odvětví potřebného k výrobě jedné jednotky v j-tém odvětví. Teorie neuronových sítí říká, že se v takové síti ustálí vzorec vzruchů, který odpovídá vahám synapsí. Výsledné úrovně vzruchů v buňkách pak představují relativní intenzity, se kterými by měla probíhat výroba v jednotlivých odvětvích. Neuronové sítě lze modelovat matematicky. Z toho plyne, že bychom měli být schopni vybilancovat ekonomiku stejnými matematickými relaxačními technikami, jaké se používají při modelování neuronových sítí. To, co musíme najít, je nějaká analogie energie, která by se dala minimalizovat.
Lidé pracující s neuronovými sítěmi často staví problém opačným způsobem - namísto pokusů o minimalizaci energie sítě maximalizují veličinu, kterou nazvali harmonie sítě. Formálně je to prostě zvratná hodnota energie, je ale intuitivně přitažlivější. Neuronová síť je uvedena do stavu maximální harmonie, když se naučí dávat „správné” odpovědi na vnější podněty.
Tento pojem harmonie můžeme aplikovat na ekonomiku. Pro každé odvětví definujme harmonickou funkci způsobem znázorněným na obrázku 6.4.
Jak je vidět, harmonie nabývá rychle záporné hodnoty, když čistý objem výroby daného odvětví (výstup po odečtení spotřeby produktu v ostatních odvětvích) je nižší než hodnota stanovená plánem. Když plán překročíme, harmonie postupně nabývá stále větší kladné hodnoty. Tím vyjadřujeme, že problémy vyvolané nedostatkem jsou závažnější, než přínosy plynoucí z přebytků. Funkce s těmito vlastnostmi může mít například konkrétní tvar, zadaný algoritmicky takto:
Nechť u = (objem výroby - cíl)/cíl.
Jestliže u < 0, pak harmonie = -u2,
jinak harmonie = √u.
Vychází se z myšlenky, že spotřebování každé další jednotky konkrétního zboží přináší lidem stále menší uspokojení. Když dostanete od příbuzného k Vánocům poprvé šálek na čaj, vaše vděčnost je upřímná; stane-li se to za sebou po páté, musíte se už trochu nutit. Z toho plyne, že přírůstek společenského uspokojení plynoucí z překračování plánovaných cílů má výrazně klesající tendenci, a že lidem bude více vadit nedostatek, než je potěší přebytek. Právě takovou situaci můžeme vymodelovat pomocí funkce harmonie, kterou jsme výše zavedli.
Když je výroba statku rovna plánované hodnotě, pak podle naší definice bude harmonie u tohoto statku rovna nule. Jestliže je výroba vyšší, harmonie je kladná, když je nižší než požaduje plán, harmonie je záporná. Tuto funkci harmonie použije počítač jako vodítko při úpravách objemů výroby. Naším úkolem je maximalizovat harmonii celé ekonomiky, uvést ji celou do rovnováhy.
Tento algoritmus způsobuje postupné vyrovnávání harmonie jednotlivých odvětví. Po pouhém tuctu iterací se průměrná harmonie každou následující iterací změní o méně než 1 procento. Má ovšem tu nevýhodu. že přivede ekonomiku pouze do lokálního maxima harmonie. Při pokusech na počítači se při této podobě algoritmu často zjistí, že někde zbyly nevyužité zdroje a že celkový objem výroby je nižší, než by měl být. Intuitivně to můžeme chápat jako důsledek velmi silné tendence algoritmu setrvávat v okolí počáteční průměrné harmonie bez ohledu na její hodnotu.
To lze překonat, jestliže algoritmus upravíme tak, aby měl sklon ke zvyšování výkonu. Namísto toho, abychom při kroku (7) snížili objem výroby odvětví s vysokou harmonií tak, aby jeho harmonie klesla na průměrnou hodnotu, upravujeme výrobu tak, aby harmonie dosáhla hodnoty (průměr + B), kde B je velikost zmíněného sklonu. Na začátku programu nastavíme vysokou hodnotu B a pak ji s každou iterací snižujeme. To způsobí, že na začátku snižují výrobu pouze odvětví s velmi vysokou počáteční harmonií, zatímco odvětví s nízkou neustále zvyšují svoji vlastní výrobu. V důsledku toho se při postupných iteracích zvyšuje průměrná harmonie, až se systém stabilizuje kolem maximální průměrné harmonie.
Při pečlivé volbě datových struktur je tento algoritmus z hlediska výpočetní doby skoro lineární. Jinými slovy, úkol se 100 odvětvími zabere desetkrát tolik času, jako úkol s 10 odvětvími. Jako u konvenční analýzy vstupů a výstupů probírané výše, je důležité nepracovat s tabulkou vstupů a výstupů jako celkem, ale využit skutečnost, že jde o velmi řídce obsazenou matici a upravit ji do formy navzájem propojených dílčích tabulek. Časová náročnost algoritmu bude pak řádu nm, kde n je počet odvětví a m průměrný počet vstupů na odvětví. Algoritmus je dostatečně jednoduchý a když byl použit k simulaci plánu pro přibližně 4000 odvětví, na pracovní stanici značky Sun trvalo řešení přibližně 300 vteřin. Pracovní stanice Sun provede asi 3 miliony instrukcí za vteřinu. Protože je program co do časové náročnosti lineární, program by na bilancování plánu pro ekonomiku s 10 miliony produktů potřeboval při použití populárního mikroprocesoru 68020 přibližně milion vteřin, tj. necelé 2 týdny. Potřeboval by také zhruba tisíc megabytů pevné paměti. To není přehnaný požadavek: je ekvivalentní asi 1000 dnešních osobních počítačů v ceně asi půl milionu liber.
Britská společnost Meiko vyvinula multiprocesor, který má až 1024 mikroprocesorovými čipů, aby dosáhla vyšších rychlostí nutných např. pro simulace ve fyzice subatomárních částic. Tento multiprocesor zvládne 10 000 000 000 instrukcí za vteřinu. Jestliže bychom náš problém mohli řešit pomocí tohoto procesoru, přičemž každý z 1024 čipů by měl 5 megabytů paměti, plán pro velkou ekonomiku by se dal vypočítat za zhruba 10 minut.
Kromě toho, že algoritmus spolehlivě určí množinu potřebných objemů výroby, jeho vedlejším důsledkem bude správná alokace kapitálových statků a surovin do jednotlivých odvětví. Právě tyto podrobné informace je třeba pro plánování.
Řekli jsme, že existují výpočetní techniky umožňující detailní plánování ekonomiky ve fyzických jednotkách bez jakékoli zmínky o penězích nebo cenách. Tyto výpočty lze zvládnout pomocí počítačů, pokud by se nasadila vysoce výkonná zařízení, jaká se dnes používají např. ve fyzice subatomárních částic nebo při předpovídání počasí. Lze je chápat jako nástroje pro předběžnou simulaci těch vyvažovacích procesů, kterých je údajně schopen idealizovaný trh.
Jeden z nejzajímavějších experimentů s plánováním a regulací pomocí počítačů byl podniknut v Chile v letech 1972 a 1973 za vlády prezidenta Allendeho. Systém navrhl Stafford Beer, který jej popsal ve své knize The Brain of the Firm.[28] Beerovým cílem bylo umožnit decentralizovanou regulaci ekonomiky v reálném čase. Jelikož jeho systém je praktickým příkladem námi navrhovaného obecného typu regulačních systémů, může být užitečné načrtnout jeho hlavní rysy.
Při konvenčních statistických metodách, které mají k dispozici vlády na Západě, jsou ekonomické statistiky v okamžiku, kdy přijdou na stoly těch, kdo rozhodují, staré už řadu měsíců. V důsledku toho se rozhodnutí k překonání krize mohou přijmout třebas až několik měsíců poté, co ke krizi skutečně došlo. Vzhledem k tomu, že politické nástroje, které má vláda k dispozici, také působí pomalu, může dojít k přijetí rozhodnutí se zcela opačným účinkem, než byl jejich původní záměr. Poté, co se v roce 1987 zhroutil trh cenných papírů, britská vláda z obavy před recesí snížila roku 1988 daně. V době, kdy tyto snížení vstoupilo v platnost ale poptávka už beztak stoupala, takže v roce 1989 bylo výsledkem zvýšení inflace. Opožděná dostupnost dat způsobila, že bylo přijato naprosto nevhodné opatření (i když v tomto případě hrálo svoji úlohu také silné ideologické zaujetí ve prospěch snižování daní, bez ohledu na makroekonomickou situaci).
Takovým zvráceným dopadům, při nichž zpětná vazba způsobuje v systému ještě větší oscilace, lze zabránit, jestliže mají regulátoři k dispozici aktuální informace a mají možnost přijmout okamžitě vhodná opatření. V Chile byla k tomuto účelu vytvořena počítačová síť. Vznikla za pouhé čtyři měsíce, k velkému překvapení skeptiků tvrdících, že její budování potrvá řadu let. Úkol byl realizován pomocí počítačové technologie z počátku 70. let a velmi omezených telekomunikačních kapacit chudé země, jakou bylo Chile. Všechna rozhodující průmyslová centra byla spojena s počítači v hlavním městě mikrovlnnými a dálnopisnými linkami. Při všech omezeních bylo možné poskytovat vládě ekonomické informace, které nebyly starší než jeden den. Modernější zařízení by to dokázalo ještě lépe.
Informace byly prezentovány ve formě ikon. V „opsroom”, operační místnosti byly instalovány velké obrazovky, které graficky znázorňovaly vzájemné interakce mezi jednotlivými sektory ekonomiky. Grafické displeje nepoužívaly žádná čísla. Velikosti toků mezi jednotlivými sektory byly vyjádřeny tloušťkou příslušných čar spojujících dané sektory. Odvětví a sektory byly znázorněny jako obdélníky obsahující sloupcové grafy, které udávaly stupeň využití kapacit příslušného odvětví. V místnosti mohlo sedět sedm lidí, což je maximální velikost skupiny, v níž se ještě všichni mohou efektivně podílet na diskusi. Tlačítky v opěradlech křesel se daly ovládat displeje a zvýrazňovat jednotlivé údaje.
Koncepce operační místnosti byla převzata z válečných zkušeností s protivzdušnou obranou. Jako za války se znázorňovaly informace v reálném čase, aby se dalo okamžitě rozhodovat. Rozhodnutí bylo možné ověřovat pomocí počítačových simulací, které ukazovaly dopady přijatých opatření. V daném případě se místnost používala jako válečný hlavní stan v boji za rozbití protivládních bojkotů vyvolávaných soukromými společnostmi pro kamionovou dopravu. Počítačová síť umožňovala vládě mobilizovat všechny dostupné dopravní prostředky k udržení toku zboží.
Záměrem bylo vytvořit operační místnost pro každé odvětví ekonomiky a samozřejmě také pro každý závod. Důmyslné statistické programy analyzovaly toky dat z nižších úrovní systému a vyhledávaly všechny významné změny. Lidé přijímající rozhodnutí byli zbaveni břemena nadměrných informací, dostávali jen signifikantní údaje, které vyžadovaly přijetí rozhodnutí. Operační místnost závodu měla být vybavena varovným systémem upozorňujícím na jakoukoli neobvyklou událost. Jestliže počítače zjistily krizový stav, vyhlásily v operační místnosti poplach a začaly odpočítávat čas. Pokud operační místnost do určité doby efektivně nezareagovala, bylo vysláno varování o stupeň vyšší operační místnosti v hierarchii systému. To dávalo každé jednotce prostor k přijetí lokálních opatření v rámci její vlastní kompetence bez ohrožení životaschopnosti sociálního organismu. Předpokládalo se, že operační místnosti na úrovni továren budou řídit místní výbory pracujících. Vycházelo se z demokratického předpokladu, že moderní vizuální a výpočetní pomůcky umožní lidem, aby vedli své továrny bez složité přípravy.
To všechno smetl krvavý převrat, který přivedl k moci Pinocheta a připravil v Chile cestu k friedmanovským monetaristickým experimentům. Operační místnost zanikla spolu s Allendem a demokracií ve vypálených ruinách prezidentského paláce.
Při revizi překladu jsem zjistil, že se autor dopustil omylu při stanovení konkrétní podoby funkce harmonie, analyticky vyjádřené jako funkce proměnné u (viz definice pod obrázkem 6.4). Rozbor vyžadující znalosti základů diferenciálního počtu vynechávám. Funkce harmonie, tak jak ji autor definuje analyticky, má podstatně jiný tvar než křivka znázorněná na obr. 6.4. V rozsahu plnění plánu od 0% do 200% má takto zvolená funkce harmonie přesně opačné vlastnosti, než ty, které požaduje autor. Produkce nad plán zvyšuje harmonii víc, než o kolik ji snižuje stejné procento neplnění plánu; při malých odchylkách od plnění na 100% je tento nepoměr dokonce extrémní (neplnění způsobuje zanedbatelný pokles harmonie, překročení její prudký růst, „hned za” bodem 100% je růst v limitě dokonce nekonečný). Tato chyba pravděpodobně vnáší do iteračního procesu nestabilitu a ztěžuje nalezení maxima; možná je také jednou z příčin, proč bylo třeba zavádět korekční faktor B. Chybu lze napravit zavedením vhodnější funkce harmonie = f(u), která pravděpodobně bude mít složitější analytické vyjádření, než funkce navrhovaná autorem. Je to technický problém, který sám o sobě nenarušuje základní myšlenku funkce harmonie, může však ztížit praktické výpočty.