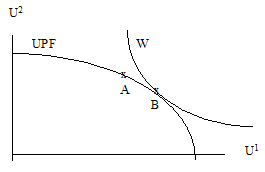
U1 a U2 jsou užitky spotřebitelů
A - některý z bodů, který prezentuje jedno z možných rozdělení užitků
B - bod blaženosti
V modelu 2x2x2x2 (dva výrobní faktory, dvě firmy, dva spotřební statky, dva spotřebitelé) lze od smluvní křivky (CC) v případě dvou výrobních faktorů (vstupů) a dvou spotřebních statků (výstupů) odvodit hranici produkčních možností (PPF). V jiném schématu (když zkoumáme případ dvou spotřebních statků a dvou spotřebitelů), máme rovněž smluvní křivku, ze které lze obdobným způsobem odvodit křivku, která je obdobou PPF a která byla nazvána hranicí dosažitelného užitku (UPF). Následně byla podniknuta snaha o interpretaci této křivky, a to patrně se snahou najít jakési odůvodnění sociálně zaměřeného přerozdělování.
Hranice dosažitelného užitku, která je odvozena od smluvní křivky, bývá interpretována takto:

U1 a U2 jsou užitky spotřebitelů
A - některý z bodů, který prezentuje jedno z možných rozdělení užitků
B - bod blaženosti
K vyjádření konfliktu mezi efektivností a spravedlností se používá křivka společenského blahobytu (W), která spojuje různé kombinace užitku dvou spotřebitelů představující stejnou úroveň společenského blahobytu. Bod dotyku UPF a (příslušné) W představuje bod blaženosti (B). Uvádí se, že tento bod je zpravidla nedosažitelný, protože pokud se chceme posunout po křivce UPF do bodu B (přerozdělit určitým způsobem příjmy spotřebitelů a tudíž i jejich užitky), můžeme např. oslabit motivy k práci a tudíž dosáhnout jen některý vnitřní bod z hlediska UPF. Tj. preferujeme-li spravedlnost, sníží se efektivnost.
Toto vysvětlení má řadu dílčích problémů, např. o následující:
Rozdělení užitků mezi dva spotřebitele je determinováno (určeno) působením samotného systému, který popisujeme. Není tedy faktorem exogenním, ale endogenním. (Tak tomu je již v původním Walrasově modelu, kdy každý jedince něco vlastní a z toho má příslušný důchod.)
Na výše naznačený problém je nutné pohlížet z hlediska interpretace reálného obsahu, který se za použitými schématy (paretovské) optimalizace skrývá. Tato schémata popisují jen jeden akt procesu použití zdrojů (vstupů) při výrobě spotřebních statků určených ke spotřebě. (Spotřeba pak končí užitkem, který chápeme jako subjektivní fenomén a vyvolání užitku je tím posledním, co v rámci příslušných schémat uvažujeme.) Takovéto omezení modelu vede k oprávněné skepsi, pokud se týká prakticky relevantních závěrů, které na základě něj můžeme formulovat.
Problém vztahu mezi efektivností a rovností (jehož součástí je mj. i otázka bohatství a chudoby, odstraňování nerovností apod.) patří mezi nejzávažnější společenské problémy vůbec a přístup k jeho řešení určuje koncepci ekonomiky veřejného sektoru, která je realizována v praxi v té či oné zemi. V oblasti teoretického pojetí vztahu mezi efektivností a rovností dochází k podstatnému posunu, který má závažné dopady i pro ekonomickou praxi.
Stávající ekonomie se domnívá, že mezi efektivní s rovností existuje rozpor, resp. substituční vztah. Dostatečně reprezentativně se k tomu vyjadřuje J. Stiglitz: "...i když je výsledek fungování tržních mechanismů efektivní, může docházet k případům, kdy je výsledné rozdělení příjmů velmi nerovnoměrné. Jedním z hlavních cílů vlády je proto ovlivnění rozložení příjmů ve společnosti." (Stiglitz, J.: Ekonomie veřejného sektoru, Grada Publishing, Praha, 1997, s.123) "...abychom dosáhli vyšší rovnosti, musíme se vzdát části efektivnosti... Například progresivní zdanění příjmů, které snižuje nerovnosti ve společnosti, snižuje podněty ke zvyšování pracovní výkonnosti, čímž snižuje efektivnost." (Stiglitz, s.124)
Grafické vyjádření výše uvedeného (Stiglitz, s. 124):
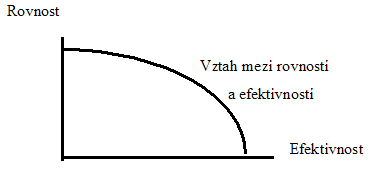
Další grafické vyjádření se týká optimalizace rozdělení užitků (Stiglitz, s. 133):
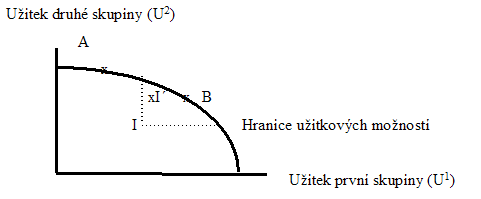
"Paretovský přístup nám bohužel nedává žádný návod, jak porovnávat rozdílné alokace zdrojů, které leží na hranici užitkových možností, například body A a B. Nemůžeme tedy říci, zda je bod A výhodnější než bod B, nebo naopak. Nemůžeme také zodpovědět otázku, zda je výhodnější snížit současné nebo budoucí sociální dávky. Nemůžeme ani ohodnotit posun z bodu pod hranicí užitkových možností (bod I) na bod ležící na hranici užitkových možností, ale ne napravo a nahoře od bodu I (bod A). Takže ačkoli alokace A je paretovsky optimální, kdežto alokace I ne, nemůžeme říci, zda je bod A výhodnější než bod I, nebo zda je tomu naopak." (Stiglitz, s. 133-134)26)
V rámci ekonomie produktivní spotřeby se nám situace jeví poněkud jinak:

Y´PF je hranice příjmových možností obou spotřebitelů, tj. maximální současná hodnota budoucího příjmu, který mohou společně dosáhnout.
Může být bod A ve výše uvedeném grafu bodem optima? Nikoli, jak je zřejmé z dalšího grafu:
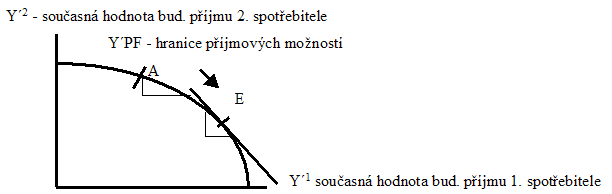
Bod optima je v tomto případě jednoznačně určen (tečnou se sklonem 45° , resp. 135° ). Přechod od bodu A k bodu E je paretovskou optimalizací. Pokud se totiž přesunujeme z bodu A směrem k bodu E, přichází druhý spotřebitel o menší část současné hodnoty budoucího příjmu, než první spotřebitel získává, tj. současná hodnota jejich společného příjmu roste. Protože za určitých podmínek si (na rozdíl od subjektivně pociťovaných užitků) mohou tento příjem přerozdělit, může si každý zvýšit současnou hodnotu budoucího příjmu (a mj. tím i svůj užitek).