Proč zrovna odmocnina?

Na tomto malém a pro výpočty nevhodném prostoru mohu jen naznačit hlavní myšlenky celého přístupu tak, aby to bylo stravitelné pro člověka s ukončeným středoškolským vzděláním a aby mu bylo patrné, proč se v politických úvahách objeví zrovna druhá odmocnina z počtu obyvatel.

Začneme předpokladem, že máme stát, který má n obyvatel. Dále předpokládejme, že zástupce tohoto státu bude v EU hlasovat o nějaké otázce ANO/NE a že se bude chovat demokraticky, tedy že svůj hlas (resp. všechny své hlasy) dá variantě ANO/NE podle toho, jak by odpověděla většina obyvatel jeho státu.

Znamená to, že se nejprve musíme zajímat o to, jak je to s počtem obyvatel daného státu, kteří by hlasovali ANO a kteří by hlasovali NE.

Budou-li obyvatelé hlasovat na sobě nezávisle, a to tak, že jich bude p% hlasovat ANO, pak lze pravděpodobnost, že právě k obyvatel bude hlasovat ANO, vyjádřit funkcí závislou na n, k a p

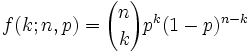
Matematici takové rozdělení nazývají binomické a té podivné závorce s n a k říkají binomický koeficient, který nahrazuje složitější výraz s faktoriály

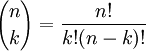
Pro úplnost připomenu, že n! (n faktoriál) je součin všech čísel od jedničky až do n, tedy

n!=1.2.3...(n-1).n

Zdá se to trochu složité, ale na příkladech se to určitě poddá.

Tak si vezměme malé království s 20 obyvateli, kteří hlasují při nepodstatném problému ANO/NE se stejnou pravděpodobností, tedy n=20 a p=50%=0,5. A podívejme se, jaká je pravděpodobnost, že jich bude ANO hlasovat právě 5, 6, 10 nebo třeba 15. Všimněte si na dalším obrázku modré křivky (horizontálně je osa k, vertikálně osa f, tedy pravděpodobnost):

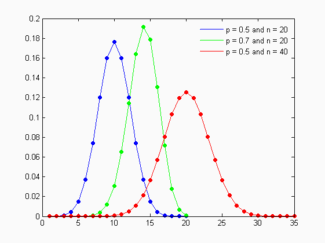
Vidíme, že nejvíc pravděpodobná je situace, že právě 10 obyvatel bude hlasovat ANO, modrá křivka má tedy při k=10 vrchol. To asi všichni čekali, jenže přesto je pravděpodobnost takové situace jen 18%!!!! S pravděpodobností 16% totiž bude hlasovat 9 obyvatel ANO a 11 NE, podobně i 11 ANO a 9 NE. Všimněte si ale, že když se vzdalujeme od nejvíce pravděpodobné hodnoty k=10, že pak pravděpodobnost prudce klesá - 5 či 15 lidí bude hlasovat ANO už jen s pravděpodobností menší než 2%.

Teď si představme, že v onom království, kde kouří právě 6 obyvatel z oněch dvaceti, se má hlasovat o otázce, zda zakázat kouření. Na tuhle otázku asi nebudou všichni hlasovat ANO/NE se stejnou pravděpodobností. Řekněme, že pravděpodobnost hlasování ANO je p=70%. Pravděpodobnost výsledku hlasování znázorňuje zelená křivka. Všimněte si, že nejpravděpodobnější výsledek hlasování je k=14 hlasů ANO (žádné překvapení), ale vidíte, že je docela možné, že těch hlasů PRO může být i 13 nebo 15. A co je pro naše další úvahy důležité, oproti minulému hlasování se příliš nemění hodnota pravděpodobnosti té nejpravděpodobnější hodnoty k=14 - stále je to 18%.

A teď pozor! Za nějakou dobu se počet obyvatel království zdvojnásobí, tedy n=40. A přijde hlasování o jiné nepodstatné otázce, kde lze znovu předpokládat pravděpodobnost odpovědi ANO p=50%. Pravděpodobnosti možných výsledků hlasování vidíte na červené křivce. Nejpravděpodobnější je, že právě polovina bude hlasovat ANO, tedy k=20. A opět je docela možné, že těch hlasů ANO bude 18, 19, 21 či 22. Červená křivka je opět podobná té modré, ale v TOMTO případě je pravděpodobnost nepravděpodobnější hodnoty JEN 12%.

A teď uděláme další myšlenkový krok a řekneme, že máme dvě království, jedno má 20, druhé 40 obyvatel a že se v nich hlasuje o té samé otázce. Snad se shodneme na tom, že i za TÉTO situace můžeme pro první A druhý stát použít modrou A červenou křivku. Podívejme se na hodnotu podílu obou maxim, tedy 18%:12%=1,5 (že tedy NENÍ roven 2), a připomeňme si, že podíl počtu obyvatel je 40:20=2. Není vůbec náhoda, že odmocnina z oněch dvou (zhruba 1,41) je blízká zjištěné hodnotě 1,5.

Rigoróznější krok pro ty, kdo mohou jít nad rámec středoškolské matematiky (ostatní nechť odsazený text přeskočí):
Předpokládáme-li p=0,5=1/2 (tedy pravděpodobnost, že každý obyvatel hlasuje ANO či NE je stejně vysoká) a zajímáme-li se o pravděpodobnost odpovídající k=n/2, spočteme
f(n/2;n,1/2)=n!/{2ⁿ[(n/2)!]²}
a následně získáme použitím Stirlingova vzorce pro velká n (splněno pro všechny státy EU)
f(n/2;n,1/2)=[2/πn]^1/2
Vidíme, že pro velká n je pravděpodobnost nejpravděpodobnějšího výsledku hlasování nepřímo úměrná právě druhé odmocnině z n.

Náš zájem o maximum (tedy nerozhodné hlasování) vyplývá z toho, že se zajímáme o situaci, kdy jedinec může teoreticky zvrátit rozhodnutí příslušného zástupce království. Jde o to, jak VELKOU má šanci, tedy pravděpodobnost ovlivnit výsledek hlasování svého zástupce, a tedy i celkový výsledek hlasování VŠECH zástupců.

Další výpočty jdou nad rámec této poznámky - jeden z nich, který jsem viděl, je veden pomocí teorie her. Tyto výpočty ale už odmocninu nepřinesou. Podstatné na těchto výpočtech je to, že se do výsledku ona odmocnina přenese - ukáže se, že s růstem počtu obyvatel vliv jednotlivého občana klesá, ale ne dramaticky jako převrácená hodnota počtu obyvatel, ale jen slaběji právě jako převrácená druhá odmocnina z počtu obyvatel. To lze ale kompenzovat tím, že zástupce daného státu dostane počet hlasů úměrný této odmocnině.

Tím se potvrdí tzv. Penroseův zákon druhé odmocniny, podle něhož je vliv každého občana na výsledek hlasování zástupců v Radě stejný za předpokladu, je síla hlasování jeho státu úměrná druhé odmocnině počtu občanů daného státu.

Milan Neubert, 5. 7. 2007